Amplitude Formula

For an object in periodic motion, the amplitude is the maximum displacement from equilibrium. For example, a pendulum swings through its equilibrium point (straight down), then swings to a maximum distance away from the center. This distance is the amplitude, A. The full range of the pendulum has a magnitude of 2A. Periodic motion also applies to things like springs and waves. The sine function oscillates between values of +1 and -1, so it is used to describe periodic motion. The unit for amplitude is meters (m).

position = amplitude x sine function(angular frequency x time + phase difference)

x = A sin(ωt + ϕ)

x = displacement (m)

A = amplitude (m)

ω = angular frequency (radians/s)

t = time (s)

ϕ = phase shift (radians)

Amplitude Formula Questions:

1) A pendulum is swinging back and forth. The angular frequency of the oscillation is ω = π radians/s, and the phase shift is ϕ = 0 radians. At time t = 8.50 s, the pendulum is 14.0 cm from its equilibrium position. What is the amplitude of the oscillation?

Answer: The position of the pendulum at a given time is the variable x, which has a value x = 14.0 cm, or x = 0.140 m. The amplitude A can be found by rearranging the formula:

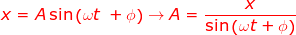
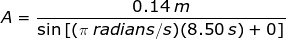
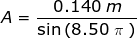
The sine of 8.50 π can be solved (keeping in mind that the value is in radians) with a calculator:

sin(8.50 π) = 1

Therefore, the amplitude at time t = 8.50 s is:

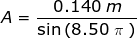
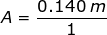
A = 0.140 m

The amplitude of the pendulum's oscillation is A = 0.140 m = 14.0 cm

2) The head of a Jack-in-the-box toy is bouncing up and down on a spring. The angular frequency of the oscillation is ω = π/6 radians/s, and the phase shift is ϕ = 0 radians. The amplitude of the bouncing is 5.00 cm. What is the position of the Jack-in-the-box head, relative to the equilibrium position, at the following times:

a) 1.00 s

b) 6.00 s

c) 11.0 s

Answer: The amplitude of the bouncing is A = 5.00 cm = 0.500 m. The position of the Jack-in-the-box head, relative to equilibrium, is x, and can be found from the formula.

a) t = 1.00 s

x = A sin(ωt + ϕ)

x = (0.500 m) sin[(π/6 radians/s)(1.00 s) + 0]

x = (0.500 m) sin(π/6 radians)

x = (0.500 m)(0.500)

x = 0.250 m

x = 2.50 cm

At time t = 1.00 s, the head is 2.50 cm above the equilibrium position.

b) t = 6.00 s

x = A sin(ωt + ϕ)

x = (0.500 m) sin[(π/6 radians/s)(6.00 s) + 0]

x = (0.500 m) sin(π radians)

x = (0.500 m)(0.00)

x = 0.00 m

At time t = 6.00 s, the head is at position x = 0.00 m, which is the equilibrium position.

c) t = 11.0 s

x = A sin(ωt + ϕ)

x = (0.500 m) sin[(π/6 radians/s)(11.0 s) + 0]

x = (0.500 m) sin(11π/6 radians)

x = (0.500 m)(-0.500)

x = -0.250 m

x = -2.50 cm

At time t = 11.0 s, the head is at position x = -2.50 cm, which is 2.50 cm below the equilibrium position.