Impulse-Momentum Theorem Formula

Impulse is a quantity that is closely related to momentum. When an object has a momentum 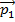, and a force is applied for an amount of time, the momentum can change to a new value 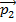. The impulse-momentum theorem states that the impulse is equal to this change in momentum. Impulse is a vector, with both a value and a direction, and is represented by the symbol 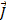. Momentum is equal to the mass times the velocity of an object (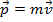). The unit of impulse is the Newton-second, 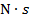, which is equivalent to .

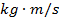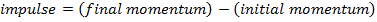
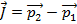
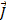= impulse (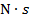, or )

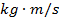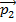= final momentum ()

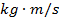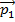= initial momentum ()

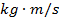Impulse-Momentum Theorem Questions:

1) A ball with a mass of 0.350 kg bounces off of a wall. Initially, it traveled horizontally to the right, toward the wall at 25.0 m/s. In then bounces, and travels horizontally to the left, away from the wall at 15.0 m/s. What is the impulse of this collision between the ball and the wall?

Answer: The first step is to define a positive direction. The problem can be solved with either the left or right horizontal direction defined as positive, but for this solution, the positive direction will be horizontally to the left (away from the wall). With this definition, the initial velocity of the ball is 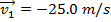(horizontally), and the final velocity of the ball is 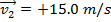(horizontally). The initial momentum is:

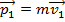
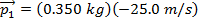
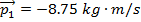
The final momentum is:

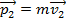
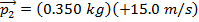
The impulse of the collision is:

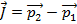
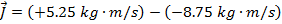
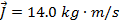
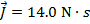
The impulse of the collision is 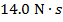, horizontally to the left.

2) A player hits a softball with a mass of 0.125 kg with a bat. Just before the impact, the ball is traveling horizontally toward the bat at 30.0 m/s. After the bat hits the ball, the ball travels horizontally, along the same path it arrived. If the impulse that affects the ball's motion is 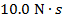horizontally away from the bat, what is the final velocity of the ball?

Answer: The first step is to define a positive direction. In this problem, the direction of the impulse is defined as horizontally away from the bat, and so this direction will be defined as positive for this solution. With this definition, the initial velocity of the ball is 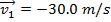(horizontally), and the final velocity of the ball, 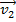, is unknown. The initial momentum is:

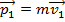
The final momentum is:

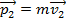
The impulse of the collision is:

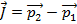
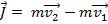
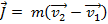
The final velocity 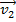can be found by rearranging this formula:

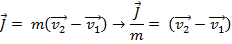
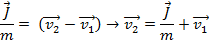
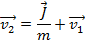
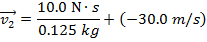
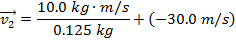
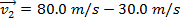
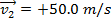
The final velocity of the ball, after colliding with the bat, is 50.0 m/s, horizontally away from the bat.