Potential Energy: Electrostatic Point Particles Formula

Potential energy is energy that is stored in a system. There is the possibility, or potential, for it to be converted to kinetic energy. Point particles with charge exert forces on each other. For opposite charges, the force is attractive. For same charges, the force is repulsive. In both cases, there is a potential energy related to the position of charges relative to each other. The unit of electric charge is the Coulomb, C. Like all work and energy, the unit of potential energy is the Joule (J), where 1 J = 1 kg m²/s² .

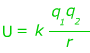
U = potential energy of electrostatic point particles

k = the Coulomb constant, k = 8.99 x 10⁹ N∙m²/C². Can be written = 1/(4πϵ₀ ) .

ϵ₀ = the permittivity of free space, ϵ₀ = 8.854 x 10^-12 C²/(N∙m² )

q₁ = charge of one of the point particles

q₂ = charge of the other point particle

r = distance between the two point charges

Potential Energy: Electrostatic Point Particles Formula Questions:

1) Two charged particles are 1.0 mm (0.0010 m) apart. One has a charge of +3.0 μC (micro-Coulombs), and the other has a charge of -8.0 μC. What is the potential energy in this two-particle system?

Answer: The potential energy can be found using the formula. The charges are given in terms of micro-Coulombs (μC): 1.0 μC = 1.0 x 10^-6 C. The charges need to be converted to the correct units before solving the equation:

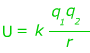
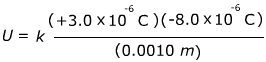
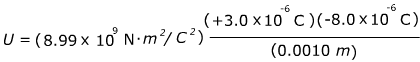
U = -215.8 N∙m

U = -215.8 J

The potential energy of this configuration is -215.8 Joules. Potential energy is always defined with reference to some position where U = 0. For this formula, the position with U = 0 is at infinite distance, so a negative sign means that these charges will move away from infinity if allowed to move freely, and therefore toward each other.

2) Two charged particles are a distance r apart. One of these particles has a charge of -5.0 μC, and the other has a charge of -1.80 μC. If the potential energy between them is U = +27.0 J, what is the distance between these particles?

Answer: The potential energy equation can be rearranged to solve for r:

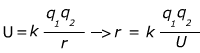
The charges are given in terms of micro-Coulombs (μC): 1.0 μC = 1.0 x 10^-6 C. The charges need to be converted to the correct units before solving the equation:

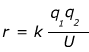
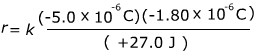
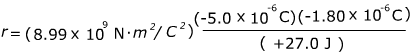
r = 0.0030 m

r = 3.0 mm

The distance between these particles is 3.0 mm.