Rotational Kinematics Formula

Motion of a rotating object can be described using formulas that relate angular displacement, angular velocity, and angular acceleration. Angular displacement is a measure of the change in the angular coordinate 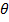, angular velocity is the rate of change of the angular coordinate with respect to time, and angular acceleration is the rate of change of angular velocity with respect to time. In these formulas, the angular acceleration is assumed to be constant. The angular coordinate and angular displacement are measured in radians. The unit of angular velocity is per second, which can be written as radians/s, 1/s, or as s^-1. The unit of angular acceleration is per second squared, which can be written as radians/s², 1/s², or as s^-2.

Angular Velocity

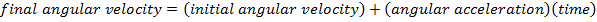
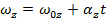
Angular Displacement

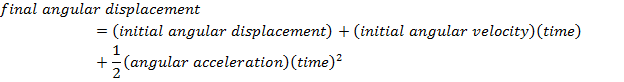
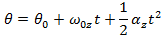
Angular Velocity, Angular Acceleration, Angular Displacement

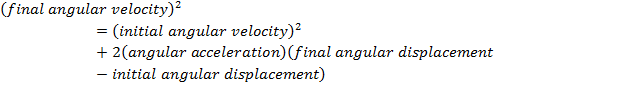
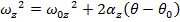
Angular Displacement and Angular Velocity

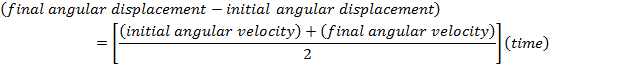
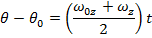
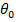= initial angular displacement, around the z axis (radians)

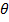= final angular displacement, around the z axis (radians)

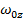= initial angular velocity, around the z axis ( radians/s, 1/s, or s^-1)

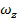= final angular velocity, around the z axis ( radians/s, 1/s, or s^-1)

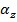= angular acceleration, around the z axis ( radians/s², 1/s², or s^-2)

t = time (s)

Rotational Kinematics Formulas Questions:

1) The disk of a computer hard drive is spinning at 750.0 radians/s at the moment the computer is turned off. The hard drive spins down at a constant negative acceleration. It takes 20.00 s to stop spinning. What was the angular displacement of the disk while it was spinning down, and how many revolutions of the disk is this equivalent to?

Answer: The first steps in a rotational kinematics problem are to identify what values are known, and then determine which formula will be the most helpful. In this problem, the initial and final angular velocities are known. The initial angular velocity is 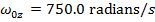, and the final angular velocity is 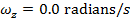(since the disk comes to a stop). The time taken for the disk to change angular velocities is given: t = 20.00 s. The initial angular displacement can be assigned to be zero: 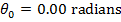. The value asked for in the question is the final angular displacement: 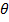. The disk's angular acceleration is not given, and so the best formula is the one that does not include it:

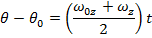
The final angular displacement can be found by rearranging this formula:

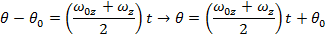
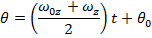
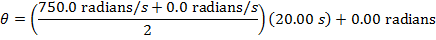
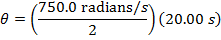
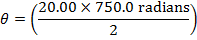
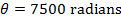
While the disk is spinning down, its angular displacement is 7500 radians. There are 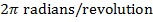, and so the number of revolutions of the disk while it is spinning down is:

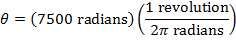
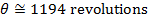
In the 20.00 s required for the disk to come to a stop, it completes nearly 1194 revolutions.

2) A potter flips a switch on her electric potter's wheel, changing it from "low" to "high" speed. This causes the wheel to accelerate at a constant angular acceleration of 4.00 radians/s². The wheel requires 80.5 radians to reach its "high" speed. If the wheel's "high" speed is 30.0 radians/s, what is the wheel's "low" speed?

Answer: The first steps in a rotational kinematics problem are to identify what values are known, and then determine which formula will be the most helpful. In this problem, the initial angular displacement can be assigned to be zero: 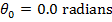. The final angular displacement is 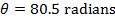. The angular acceleration is 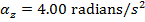. The final angular velocity is 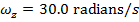. The initial angular velocity 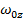is unknown, and asked for in the problem. The amount of time required is not known, and so the best formula is the one that does not include time t:

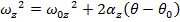
The wheel's initial angular velocity can be found by rearranging this formula:

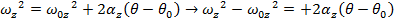
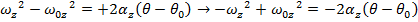
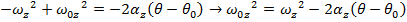
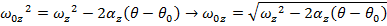
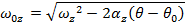
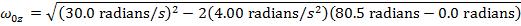
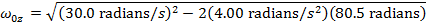
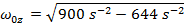
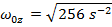
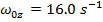
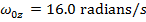
The angular velocity of the "low" speed setting of the potter's wheel is 16.0 radians/s.