Torque Formula (Force at a Distance)

A force that acts on a moment arm, and is used to cause rotational motion is called torque. Torque is the cross product of a length and a force. The length is between a center of rotation and the point where a force is applied. The cross product can only be applied between two vectors (magnitude and direction). The solution to a cross product is: 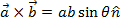, where 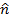is a vector that is perpendicular to the other two. The Greek letter tau (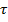) is used to represent it. The units of torque are Newton-meters (N∙m).

torque = (distance between a center of rotation and a force) x (force)

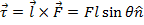
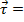= torque (N∙m)

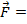= force vector (N)

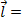= length vector, directed from the center of rotation to the force point (meters)

Torque Formula Questions:

1) A car mechanic applies a force of 800 N to a wrench to loosen a bolt. She applies the force perpendicular to the arm of the wrench. The distance from the bolt to her hand is 0.40 m. What is the magnitude of the torque applied?

Answer: The angle between the moment arm (the arm of the wrench) and the force is 90°, and sin 90° = 1. The torque is:

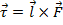
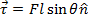
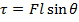
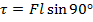
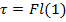
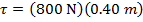
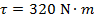
The magnitude of the torque is 320 N∙m.

2) An anemometer is a device to measure wind speed. It has a number of metal cups mounted on horizontal bars that turn a center rod. The wind catches one of the cups, perpendicular to its horizontal bar. The wind exerts a 70.0 N force on the cup, at a distance of 0.30 m from the central axis. What is the magnitude of the torque applied by the wind?

Answer: The angle between the moment arm (the horizontal bar) and the force is 90°, and sin 90° = 1. The torque is:

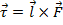
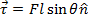
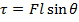
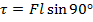
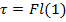
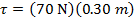
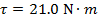
The magnitude of the torque is 21.0 N∙m.