Clearing Equations of Fractions
|
When equations have a lot of fractions in them, the easiest way to solve them is to first clear all the fractions. In order to do this, you must multiply every term by the LCD (least common denominator).
In case you forgot how to find the LCD, you have to think of a number that can be evenly divided by each of the denominators. For example, if the denominators are 6, 5, and 10, the smallest number that can be evenly divided by all of these is 30. Now, if you thought of 60, that is not the least common denominator, but it is a common denominator, so it will work. You will just have to reduce at the end. Let's try a problem: 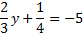 The first step is to clear this equation of fractions by multiplying by the LCD. The LCD is 12, so we will multiply every term on both sides by 12. 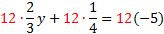 Now we need to multiply each term, and if we chose the right LCD, all the fractions will be gone. 8y+3=-60 With the fractions gone, we can proceed as normal: 8y+3-3=-60-3 8y=-63 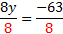 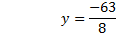 Let's look at another problem. We'll start by determining the LCD and multiplying it by every term. 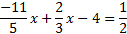 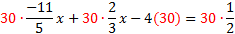 Notice that we had to be careful to also distribute the 30 to the -4. Now we need to simplify each term. -66x+20x-120=15 With the fractions gone, we can proceed as normal:
-66x+20x-120=15 -46x-120=15 -46x-120+120=15+120 -46x=135 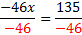 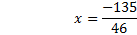 Practice:Eliminate the fractions then solve the equation. 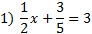 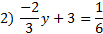 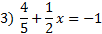 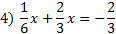 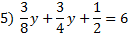 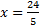 2)
2)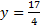 3)
3)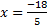 4)
4)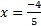 5)
5)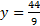 |
|
Related Links: Math Algebra Factors |
