Completing the Square: Circles
This is the pattern from which we can glean information to graph a circle. But the equations are not always listed in this format. In this case, you need to rearrange them to match the pattern. You can do this with a process called completing the square.
To rearrange the equation.....
1. Move any constant terms to the right hand side
2. Find the coefficients of the first degree term (x)
3. Divide the coefficient by two then square it.
4. Add that number to both sides of the equation
5. Factor the resulting trinomial
6. Repeat steps #2-5 with y
7. Rearrange the terms if needed
Let's look at a few examples to see how these steps work. We will rearrange each equation to match the pattern for graphing.2. Find the coefficients of the first degree term (x)
3. Divide the coefficient by two then square it.
4. Add that number to both sides of the equation
5. Factor the resulting trinomial
6. Repeat steps #2-5 with y
7. Rearrange the terms if needed
1.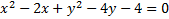
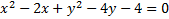
First we needto move the constant (-4) to the other side:
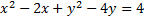
The coefficient of x is -2. We need to take that number, divide it by 2 and square it.
-2/2 = -1 then (-1)2 = 1
We must add that number to both sides. We'll want to add it by the -2x term to create a trinomial:
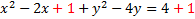
Now we'll factor the trinomial (shown in green)
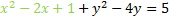
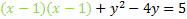
If we did everything correctly, factoring should always produce a perfect square. Let's rewrite it:
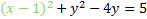
Now we'll repeat the process for the y. We start by finding the coefficient of the first degree term, which is -4. We divide it by 2 then square it. -4/2=-2then (-2)2=4. We'll add this to both sides:
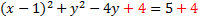
Next we factor the trinomial:
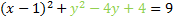
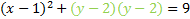
And rewrite it:
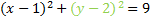
This matches our pattern, so this is our final answer: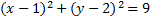
We would now be able to easily find the center and radius.
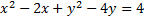
The coefficient of x is -2. We need to take that number, divide it by 2 and square it.
-2/2 = -1 then (-1)2 = 1
We must add that number to both sides. We'll want to add it by the -2x term to create a trinomial:
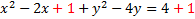
Now we'll factor the trinomial (shown in green)
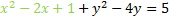
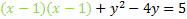
If we did everything correctly, factoring should always produce a perfect square. Let's rewrite it:
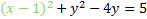
Now we'll repeat the process for the y. We start by finding the coefficient of the first degree term, which is -4. We divide it by 2 then square it. -4/2=-2then (-2)2=4. We'll add this to both sides:
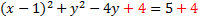
Next we factor the trinomial:
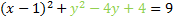
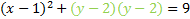
And rewrite it:
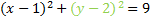
This matches our pattern, so this is our final answer:
We would now be able to easily find the center and radius.
2.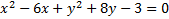
Practice: Rearrange each of the following circles to match the pattern for graphing.
First we want to move the constant (-3) to the other side:
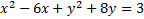
The coefficient of xis -6. We need to take that number, divide it by 2 and square it.
-6/2 = -3 then (-3)2 = 9
We must add that number to both sides. We'll want to put it by the -6x term to create a trinomial:
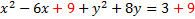
Now we'll factor the trinomial (shown in green)
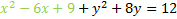
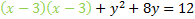
If we did everything correctly, factoring should always produce a perfect square. Let's rewrite it:
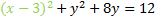
Now we'll repeat the process for the y. We start by finding the coefficient of the first degree term, which is 8. We divide it by 2 then square it. 8/2=4then (4)2=16. We'll add this to both sides:
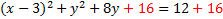
Next we factor the trinomial:
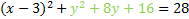
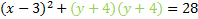
And rewrite it:
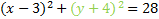
This matches our pattern, so this is our final answer: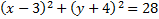
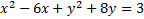
The coefficient of xis -6. We need to take that number, divide it by 2 and square it.
-6/2 = -3 then (-3)2 = 9
We must add that number to both sides. We'll want to put it by the -6x term to create a trinomial:
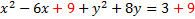
Now we'll factor the trinomial (shown in green)
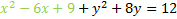
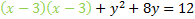
If we did everything correctly, factoring should always produce a perfect square. Let's rewrite it:
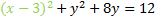
Now we'll repeat the process for the y. We start by finding the coefficient of the first degree term, which is 8. We divide it by 2 then square it. 8/2=4then (4)2=16. We'll add this to both sides:
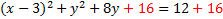
Next we factor the trinomial:
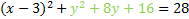
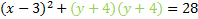
And rewrite it:
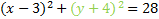
This matches our pattern, so this is our final answer:
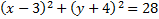
1. 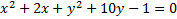
2.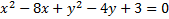
3.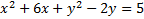
4.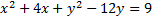
5.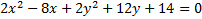 Hint: Divide each term by 2 first
Hint: Divide each term by 2 first
Answers:
1) 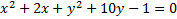
2.
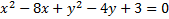
3.
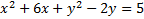
4.
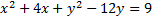
5.
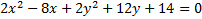 Hint: Divide each term by 2 first
Hint: Divide each term by 2 first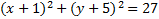 2)
2) 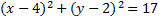 3)
3) 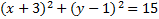 4)
4) 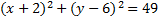 5)
5) 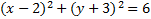
|
Related Links: Math Fractions Factors |
