Completing the Square: Ellipses and Hyperbolas
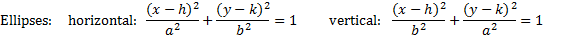
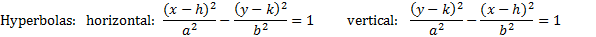
When the equation is not in this graphing format, you must first rearrange it by completing the square.
To complete the square for ellipses and hyperbolas:
1. Arrange the equation so all the terms with variables are on the same side and the constant is on the other side.
2. Rearrange the terms so that the y terms are together and the x terms are together.
3. Factor out the coefficient of the x2 term and the y2 term.
4. For each set (x and y separately), take the number in front of the first degree term, divide it by 2 and square it.
5. Add both number's values to both sides of the equation. (Be careful: You have to add the number's full distributed value.)
6. Factor both trinomials and rewrite them.
7. Simplify the right hand side and divide each term by that number so that the right hand side equals 1.
8. Simplify and rearrange as needed to match the pattern.
Examples: 2. Rearrange the terms so that the y terms are together and the x terms are together.
3. Factor out the coefficient of the x2 term and the y2 term.
4. For each set (x and y separately), take the number in front of the first degree term, divide it by 2 and square it.
5. Add both number's values to both sides of the equation. (Be careful: You have to add the number's full distributed value.)
6. Factor both trinomials and rewrite them.
7. Simplify the right hand side and divide each term by that number so that the right hand side equals 1.
8. Simplify and rearrange as needed to match the pattern.
1. 9x2-18x+16y2+96y+9=0
Practice: Rearrange each equation into the graphing format by completing the square:
First, we need to arrange the equation with all the variables on one side and the constant on the other. That means we need to move the 9 to the other side.
We must add each of these values to both sides of the equation. For x, when we add the 1 in parenthesis, we are really adding 9 (because 9 is distributed to the 1). Thus, we must add 9 to the right hand side:
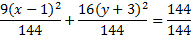 And simplify:
And simplify:
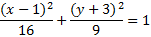 Now it is in a format from which we can clean our information.
Now it is in a format from which we can clean our information.
2. 9x2+36x-y2+10y+2=09x2-18x+16y2+96y = -9
The x and y terms are already grouped together, so we now need to factor out the coefficient of the x2 term and the y2 term. We will factor the x's and y's separately: 9(x2-2x)+16(y2+6y)= -9
Now we take the number in from of the first degree term, divide it by 2 and square it. For x, -2 divided by 2 is -1, squared is 1. For y, 6 divided by 2 is 3, squared is 9.We must add each of these values to both sides of the equation. For x, when we add the 1 in parenthesis, we are really adding 9 (because 9 is distributed to the 1). Thus, we must add 9 to the right hand side:
9(x2-2x+1)+16(y2+6y)=-9+9
For y, we must add 9 in parenthesis. This is really adding 144 (because 16 is distributed to the 9.) Thus, we'll add 144 to the right hand side.9(x2-2x+1)+16(y2+6y+9)=-9+9+144
Now we'll factor each trinomial9(x-1)(x-1)+16(y+3)(y+3)=144
And rewrite them:9(x-1)2+16(y+3)2=144
We need the right hand side to be 1, so we will divide each term by 144.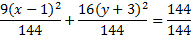
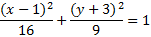
First, we need to arrange the equation with all the variables on one side and the constant on the other. That means we need to move the 2 to the other side.
We must add each of these values to both sides of the equation. For x, when we add the 4 in parenthesis, we are really adding 36 (because 9 is distributed to the 4). Thus, we must add 36 to the right hand side:
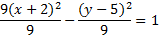 And simplify:
And simplify:
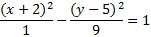 Now it is in a format from which we can clean our information.
Now it is in a format from which we can clean our information.
9x2+36x-y2+10y = -2
The x and y terms are already grouped together, so we now need to factor out the coefficient of the x2term and the y2 term. We will factor the x's and y's separately: 9(x2+4x)-(y2-10y)= -2
Now we take the number in from of the first degree term, divide it by 2 and square it. For x, 4 divided by 2 is 2, squared is 4. For y, -10 divided by 2 is -5, squared is 25.
We must add each of these values to both sides of the equation. For x, when we add the 4 in parenthesis, we are really adding 36 (because 9 is distributed to the 4). Thus, we must add 36 to the right hand side:
9(x2+4x+4)-(y2-10y)= -2+36
For y, we must add 25 in parenthesis. This is really adding -25 (because the negative is distributed to the 25.) Thus, we'll add -25 to the right hand side. 9(x2+4x+4)-(y2-10y+25)= -2+36-25
Now we'll factor each trinomial9(x+2)(x+2)-(y-5)(y-5)=9
And rewrite them:9(x+2)2-(y-5)2=9
We need the right hand side to be 1, so we will divide each term by 9.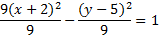
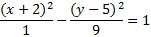
1. 4x2+32x+9y2-36y+64 = 0
2. x2+2x+16y2-96y+129=0
3. 9x2-90x+y2+6y+225=0
4. 9x2+18x-25y2-50y-241=0
5. -x2-4x+4y2+24y+16=0
Answers:
1) 2. x2+2x+16y2-96y+129=0
3. 9x2-90x+y2+6y+225=0
4. 9x2+18x-25y2-50y-241=0
5. -x2-4x+4y2+24y+16=0
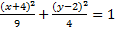 2)
2) 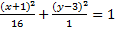 3)
3) 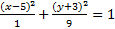
4)
 5)
5) 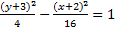
|
Related Links: Math Fractions Factors |
