Finding Horizontal Asymptotes of Rational Functions

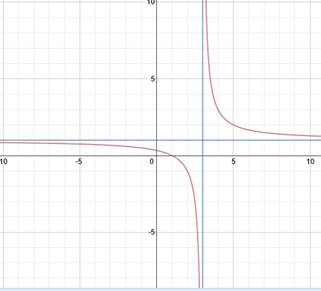
Remember that an asymptote is a line that the graph of a function approaches but never touches. Rational functions contain asymptotes, as seen in this example:

$Finding horizontal asymptotes of rational functions img 1$

In this example, there is a vertical asymptote at x = 3 and a horizontal asymptote at y = 1. The curves approach these asymptotes but never cross them.

The method used to find the horizontal asymptote changes depending on how the degrees of the polynomials in the numerator and denominator of the function compare.

If both polynomials are the same degree, divide the coefficients of the highest degree terms.

Example:

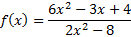
$Finding horizontal asymptotes of rational functions img 2$
Both polynomials are 2^nd degree, so the asymptote is at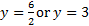 $Finding horizontal asymptotes of rational functions img 3$
If the polynomial in the numerator is a lower degree than the denominator, the x-axis (y = 0) is the horizontal asymptote.

If the polynomial in the numerator is a higher degree than the denominator, there is no horizontal asymptote. There is a slant asymptote, which we will study in a later lesson.

Examples: Find the horizontal asymptote of each rational function:

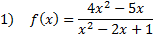
$Finding horizontal asymptotes of rational functions img 4$

First we must compare the degrees of the polynomials. Both the numerator and denominator are 2^nd degree polynomials. Since they are the same degree, we must divide the coefficients of the highest terms.

In the numerator, the coefficient of the highest term is 4.

In the denominator, the coefficient of the highest term is an understood 1.

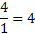
$Finding horizontal asymptotes of rational functions img 5$

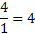
The horizontal asymptote is at y = 4.

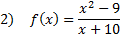
$Finding horizontal asymptotes of rational functions img 6$

First we must compare the degrees of the polynomials. The numerator contains a 2^nd degree polynomial while the denominator contains a 1^st degree polynomial.

Since the polynomial in the numerator is a higher degree than the denominator, there is no horizontal asymptote. There is a slant asymptote instead.

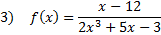
$Finding horizontal asymptotes of rational functions img 7$

First we must compare the degrees of the polynomials. The numerator contains a 1^st degree polynomial while the denominator contains a 3^rd degree polynomial.

Since the polynomial in the numerator is a lower degree than the denominator, the horizontal asymptote is located at y=0.

Practice: Find the horizontal asymptote of each rational function.

$Finding horizontal asymptotes of rational functions img 8$

$Finding horizontal asymptotes of rational functions img 9$

$Finding horizontal asymptotes of rational functions img 10$

$Finding horizontal asymptotes of rational functions img 11$

$Finding horizontal asymptotes of rational functions img 12$

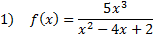
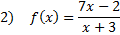
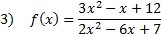
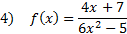
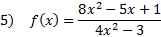
Answers: 1) None 2) y = 7 3) 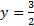$Finding horizontal asymptotes of rational functions img 13$ 4) y = 0 5) y = 2

Related Links:
Math
Fractions
Factors

Finding Horizontal Asymptotes of Rational Functions

More Topics

Educational Videos