Solving More Complex Logarithmic Equations
1. If you have the same logarithm on both sides, their arguments will equal
each other.
Example: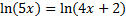 
Since the base of the natural log is e, we will raise both sides to be powers of e.
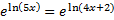
On both sides, the e and ln cancel leaving us with this:
5x = 4x + 2
As you can see, the arguments (the value inside parenthesis) equal each other. You can remember this shortcut or you can simply follow the normal procedure as we just did.
Now we can proceed to solve the equation:
x = 2
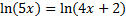
Since the base of the natural log is e, we will raise both sides to be powers of e.
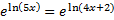
On both sides, the e and ln cancel leaving us with this:
5x = 4x + 2
As you can see, the arguments (the value inside parenthesis) equal each other. You can remember this shortcut or you can simply follow the normal procedure as we just did.
Now we can proceed to solve the equation:
x = 2
2) Sometimes an apparent solution is not valid.
Remember that for a logarithm with a positive base the argument (value inside parenthesis) must be positive. Thus, if the solution for x results in a negative argument, the solution is not valid.
Example: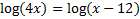
In this case, the arguments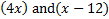
must both be greater than or equal to 0. When we find our solution, we will check them to make sure this is true.
Let's solve the equation. Since we have a common log on both sides, the arguments equal each other:
4x = x - 12
3x = -12
x = -4
Let's put -4 back into the arguments. We get log(-16) on both sides. But this is impossible since 10 cannot be raised to a power and result in a negative number. This is not a valid answer.
Thus, this equation has no solution.
Example:
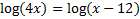
In this case, the arguments
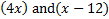must both be greater than or equal to 0. When we find our solution, we will check them to make sure this is true.Let's solve the equation. Since we have a common log on both sides, the arguments equal each other:
4x = x - 12
3x = -12
x = -4
Let's put -4 back into the arguments. We get log(-16) on both sides. But this is impossible since 10 cannot be raised to a power and result in a negative number. This is not a valid answer.
Thus, this equation has no solution.
3) Sometimes you must use log rules.
Example: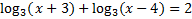 
Since the logs are being added, we must multiply their arguments:
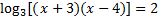
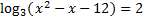
And solve:
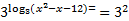
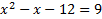
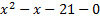
We must solve this with the quadratic formula.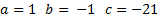
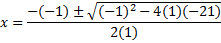
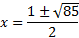
This is the exact answer. Or we can estimate using our calculator:
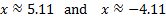
Since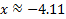
results in a negative argument, this is not a solution
Answer: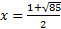
or 
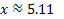
Practice: Solve each logarithmic equation. Make sure each solution is valid. If necessary, round your answer to the nearest thousandth.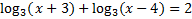Since the logs are being added, we must multiply their arguments:
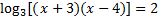
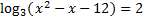
And solve:
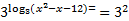
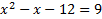
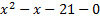
We must solve this with the quadratic formula.
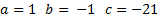
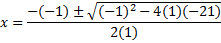
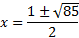
This is the exact answer. Or we can estimate using our calculator:
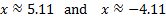
Since
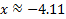results in a negative argument, this is not a solutionAnswer:
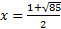or 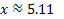1)
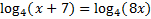
2)
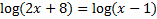
3)
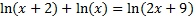
4)
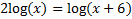
5)
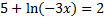
Answers: 1) x = 1 2) no solution 3) x = 3 4) x = 3 5)
|
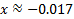
Related Links: Math Fractions Factors |