Solving Triangles
To solve a triangle means that you find the measure of each angle and the length of each side.
Depending on what information you are given, you must start with either the Law of Sines or the Law of Cosines.
If you know..... Use.....
SSS Law of Cosines
SAS Law of Cosines
SSA Law of Sines*
AAS Law of Sines
ASA Law of Sines
SSS Law of Cosines
SAS Law of Cosines
SSA Law of Sines*
AAS Law of Sines
ASA Law of Sines
*Watch for the ambiguous case
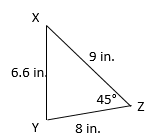
Solve this triangle:
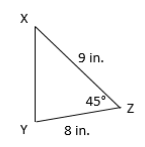
We need to find
, 
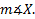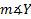, and the length of side z. Let's take them one at a time.1) First we'll use the Law of Cosines to find the length of side z.
We know we need to use the Law of Cosines because we are have SAS (two sides and the angle in between.)
C will be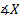
or 45°. a and b are 9 and 8. Let's substitute and solve:
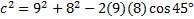
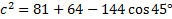
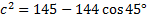
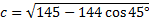
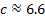
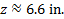
C will be
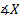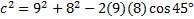
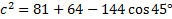
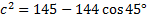
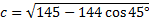
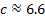
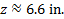
or 45°. a and b are 9 and 8. Let's substitute and solve:2) Now we need to find
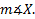
Let's input our new info into our triangle:
We can use either the Law of Sines or the Law of Cosines. Let's use the Law of Sines (rewritten to portray angles X, Y, and Z instead of A, B, and C)
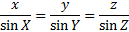
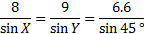
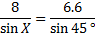
8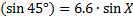
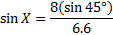
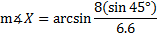
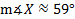
We can use either the Law of Sines or the Law of Cosines. Let's use the Law of Sines (rewritten to portray angles X, Y, and Z instead of A, B, and C)
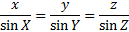
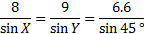
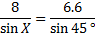
8
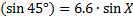
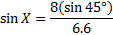
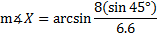
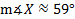
3) Find
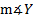
Since we know that the three angles of a triangle add up to 180°, we can subtract the two known angles to find the third:
180° - 45° - 59° = 76°
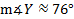
180° - 45° - 59° = 76°
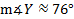
Now this answer assumes we found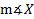 
correctly. To double check your answer, you can find 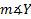using either the Law of Sines or the Law of Cosines. If that answer also comes out around 76°, you can be fairly confident that you did everything correctly. Note, however, that both answers are dependent upon your calculation of side z, and z was rounded to the tenths place. Thus, there will be some variety in the answer due to rounding error. To reduce this, keep the value for z in the memory of your calculator and use this value instead of the rounded 6.6 in the final calculation.
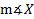correctly. To double check your answer, you can find 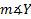using either the Law of Sines or the Law of Cosines. If that answer also comes out around 76°, you can be fairly confident that you did everything correctly. Note, however, that both answers are dependent upon your calculation of side z, and z was rounded to the tenths place. Thus, there will be some variety in the answer due to rounding error. To reduce this, keep the value for z in the memory of your calculator and use this value instead of the rounded 6.6 in the final calculation.Practice: Solve these triangles. Round all answers to the nearest tenth.
#1-3: Solve triangle XYZ
#4-6: Solve triangle DEF
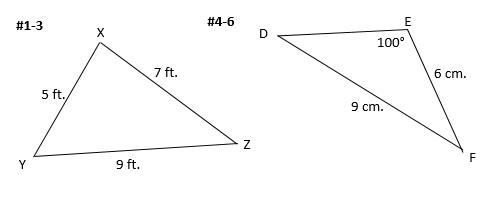
Answers: (Note: Answers may vary slightly due to differences in rounding.)
#1-3)
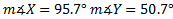
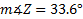#4-6)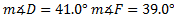 
f = 5.8 cm.
|
Related Links: Math Fractions Factors |