Understanding Circles
The equation of a circle follows this pattern
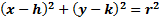
In this pattern, (h, k) is the center of the circle and r is the radius.
Before you can graph a circle, you must understand how to find the center point and the radius.
Let's look at a couple examples.
1. Find the center point and radius of this circle:
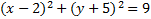
Notice in the pattern that there is a negative in front of both the h and the k. Since the negative is part of the pattern, you must take the opposite of each of these numbers in order to find the center point. So in this example, 2 is h and -5 is k. (Notice that both signs changed.) Thus our center point is (2,-5)
Now 9 = r2, so we'll need to take the square root to find r. The square root of 9 is 3, so the radius is 3.
Answer: Center point (2,-5), radius = 3
Now 9 = r2, so we'll need to take the square root to find r. The square root of 9 is 3, so the radius is 3.
Answer: Center point (2,-5), radius = 3
2. Find the center point and radius of this circle:
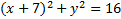
The h in this is -7 because we have to take the opposite of 7. But what is the k? To answer that, let's look at that part of the pattern: 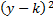 The only number that could possibly be k in this situation is 0 because
The only number that could possibly be k in this situation is 0 because
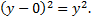 . Since 0 is the identity number for addition, whenever there is no number specifically listed as h or k, it will be 0. So k = 0 and our center point is (-7,0).
. Since 0 is the identity number for addition, whenever there is no number specifically listed as h or k, it will be 0. So k = 0 and our center point is (-7,0).
For the radius, remember 16 is not the radius. 16 is the radius squared. Taking the square root, we find that r = 4.
Answer: Center point (-7,0) , radius = 4.
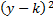 The only number that could possibly be k in this situation is 0 because
The only number that could possibly be k in this situation is 0 because
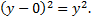 . Since 0 is the identity number for addition, whenever there is no number specifically listed as h or k, it will be 0. So k = 0 and our center point is (-7,0).
. Since 0 is the identity number for addition, whenever there is no number specifically listed as h or k, it will be 0. So k = 0 and our center point is (-7,0).For the radius, remember 16 is not the radius. 16 is the radius squared. Taking the square root, we find that r = 4.
Answer: Center point (-7,0) , radius = 4.
Practice: Find the center point and radius of each of these circles.
1.
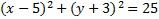
2.
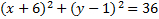
3.
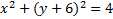
4.
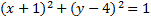
5.
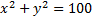
Answers: 1)
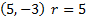 2)
2)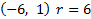 3)
3)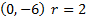 4)
4)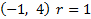 5)
5)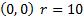
|
Related Links: Math Fractions Factors |
