Understanding Ellipses
There are two patterns for an ellipse:
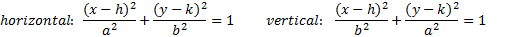
In both patterns, (h, k) is the center point, just as it was with a circle.
The a and the b have to do with how wide and how tall the ellipse is.
Each ellipse has a major axis and a minor axis. The major axis is the line that goes through the longest length of the ellipse. The minor axis goes through the shorter distance.
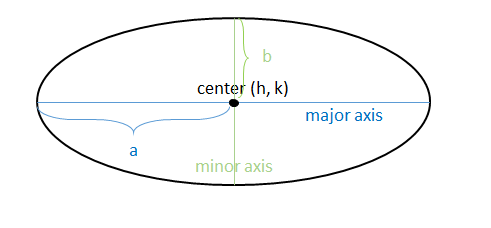
The major axis is always associated with the variable a and equals 2a. (a is the distance from the center point to the ellipse along the major axis, so you have to double that to get the length of the entire axis.)
The minor axis is always associated with b and equals 2b. (b is the distance from the center point to the ellipse along the minor axis, so once again you have to double that to get the length of the entire axis.)
You'll notice e there are two different patterns: one for a horizontal ellipse and one for a vertical. Whichever denominator is larger determines which variable is a (because a is always bigger since it is the major axis.) If the larger number is under the x, then the ellipse is horizontal. If it is under the y then it is vertical.
Let's look at a couple ellipses and see what we can tell about them.
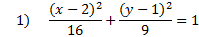
Let's start by finding the center point. Remember that since there is a negative in the pattern, we must take the opposite of each, just as we did with circles. h is 2 (opposite of -2) and k is 1 (opposite of -1). Thus our center point is (2, 1)
Now we need to decide if this ellipse is vertical or horizontal. To tell that, we look and see which denominator is larger. 16 is larger than 9, so that means 16 is a2 (since it is larger). Whenever the larger number (a2) is underneath the x, then it is a horizontal ellipse. (You can remember this because the x-axis is the horizontal axis.)
We want to identify one last piece of information: the length of a and b. Notice in the pattern that both of these are squared, so we have to take the square root of each. The square root of 16 is 4 and the square root of 9 is 3. Thus, a = 4 and b = 3
Summary: This is a horizontal ellipse with a center point of (2, 1). a = 4 and b = 3
Now we need to decide if this ellipse is vertical or horizontal. To tell that, we look and see which denominator is larger. 16 is larger than 9, so that means 16 is a2 (since it is larger). Whenever the larger number (a2) is underneath the x, then it is a horizontal ellipse. (You can remember this because the x-axis is the horizontal axis.)
We want to identify one last piece of information: the length of a and b. Notice in the pattern that both of these are squared, so we have to take the square root of each. The square root of 16 is 4 and the square root of 9 is 3. Thus, a = 4 and b = 3
Summary: This is a horizontal ellipse with a center point of (2, 1). a = 4 and b = 3
2) Tell if this ellipse is horizontal or vertical and find its center point, a, and b.
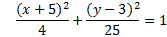
Let's start by finding the center point. Remember that since there is a negative in the pattern, we must take the opposite of each. h is -5 (opposite of 5) and k is 3 (opposite of -3). Thus our center point is (-5, 3)
Now we need to decide if this ellipse is vertical or horizontal. To tell that, we look and see which denominator is larger. 25 is larger than 4, so that means 25 is a2 (since it is larger). Whenever the larger number (a2) is underneath the y, then it is a vertical ellipse. (We can remember this because the y-axis is the vertical axis.)
Now let's find a and b. Remember that we have to take the square root of each. The square root of 25 is 5 and the square root of 4 is 2. Thus, a = 5 and b = 2
Summary: This is a vertical ellipse with a center point of (-5, 3). a = 5 and b = 2
Now we need to decide if this ellipse is vertical or horizontal. To tell that, we look and see which denominator is larger. 25 is larger than 4, so that means 25 is a2 (since it is larger). Whenever the larger number (a2) is underneath the y, then it is a vertical ellipse. (We can remember this because the y-axis is the vertical axis.)
Now let's find a and b. Remember that we have to take the square root of each. The square root of 25 is 5 and the square root of 4 is 2. Thus, a = 5 and b = 2
Summary: This is a vertical ellipse with a center point of (-5, 3). a = 5 and b = 2
Practice: Tell if each ellipse is horizontal or vertical. Then find the center point, a, and b.
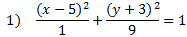
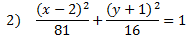
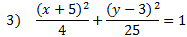
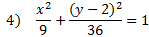
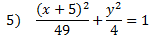
Answers:
1) Vertical, center (5, -3) a = 3, b = 1
2) Horizontal, center (2, -1) a = 9, b = 4
3) Vertical, center (-5, 3) a = 5, b = 2
4) Vertical, center (0, 2) a = 6, b = 3
5) Horizontal, center (-5, 0) a = 7, b = 2
2) Horizontal, center (2, -1) a = 9, b = 4
3) Vertical, center (-5, 3) a = 5, b = 2
4) Vertical, center (0, 2) a = 6, b = 3
5) Horizontal, center (-5, 0) a = 7, b = 2
|
Related Links: Math Fractions Factors |
