Understanding the Pythagorean Identities

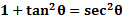
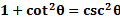
These are derived from the Pythagorean Theorem and the unit circle. And they are very useful when for manipulating and solving equations.
Before you can use these to solve equations, you must understand how to manipulate them.
Examples:
1) Simplify
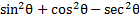 using the Pythagorean identities
using the Pythagorean identities
Since we know that 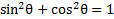 we can replace
we can replace 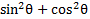 with 1:
with 1:

This is good, but we can go even further. If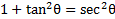 then we can rearrange this identity by moving the 1 to the other side:
then we can rearrange this identity by moving the 1 to the other side: 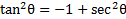 and then multiplying both sides by -1:
and then multiplying both sides by -1: 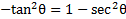 . Thus, our expression actually equals:
. Thus, our expression actually equals:
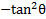
Being able to manipulate expressions will be helpful when solving more complex equations.
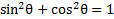 we can replace
we can replace 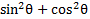 with 1:
with 1:
This is good, but we can go even further. If
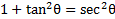 then we can rearrange this identity by moving the 1 to the other side:
then we can rearrange this identity by moving the 1 to the other side: 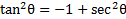 and then multiplying both sides by -1:
and then multiplying both sides by -1: 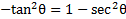 . Thus, our expression actually equals:
. Thus, our expression actually equals: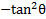
Being able to manipulate expressions will be helpful when solving more complex equations.
2) Rewrite
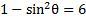 to contain a cos function instead of a sin function.
to contain a cos function instead of a sin function.We can replace 1 with 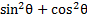 :
:
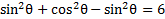
Now we can add like terms.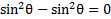 . Thus our equation is now:
. Thus our equation is now:
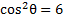
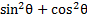 :
: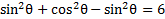
Now we can add like terms.
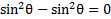 . Thus our equation is now:
. Thus our equation is now:
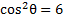
3) Simplify
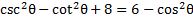 and rewrite it to contain only a sin function.
and rewrite it to contain only a sin function.First, since 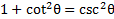 , let's replace
, let's replace 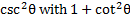
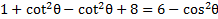
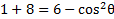
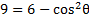
We know that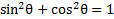 , but there is no 1 to replace. However, if we subtract 5 from both sides then there will be.
, but there is no 1 to replace. However, if we subtract 5 from both sides then there will be.
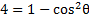
Now we can substitute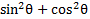 for the 1
for the 1

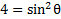
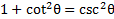 , let's replace
, let's replace 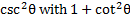
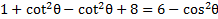
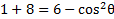
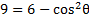
We know that
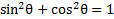 , but there is no 1 to replace. However, if we subtract 5 from both sides then there will be.
, but there is no 1 to replace. However, if we subtract 5 from both sides then there will be.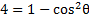
Now we can substitute
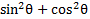 for the 1
for the 1
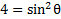
Practice: Use the Pythagorean Identities to rewrite the following expressions as instructed:
1) Simplify
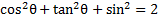
2) Simplify
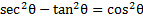
3) Rewrite this expression to include sin instead of cos:
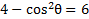
4) Rewrite this expression to include cot instead of csc:
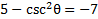
5) Simplify
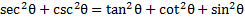
Answers (Equivalent answers are also possible)
1)
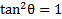 2)
2) 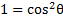 3)
3) 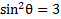 4)
4) 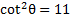 5)
5) 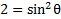
|
Related Links: Math Fractions Factors |
