Understanding the Sum-Difference Formulas
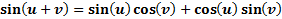
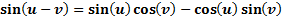
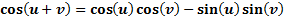
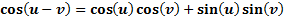
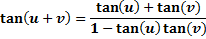
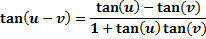
These formulas can be helpful in rearranging expressions in order to be able to solve complex equations. They are not difficult formulas to use, but you do need to be careful to follow them exactly. Let's examine some examples to see how they can work.
1)
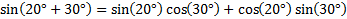
Obviously we could simply use a calculator to find the sine, but this example helps us easily see how the formula works.
2) Rearrange this trig identity using the sum-difference formulas:
cos(A - B)
We need to carefully follow the pattern of the formula.
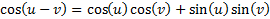
In our problem, u is A and v is B:

3) Rearrange this trig identity to include a 10° angle.
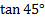
At first glance, this identity does not include a 10° angle. However, we could rewrite 45° as 35° + 10°:
tan 45° = tan(35°+10°)
And then apply the formula:
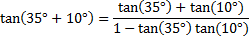
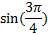
We must use a difference identity because 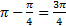
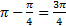
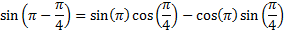
Practice: Rearrange each identity as instructed using the angle-sum and angle-difference formulas:
1) Rearrange

2) Rearrange
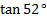 to include a 25° angle.
to include a 25° angle.3) Rearrange
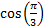 to include an angle that is ∏ radians.
to include an angle that is ∏ radians.4) Rearrange
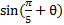
5) Rearrange
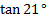 to include a 90° angle.
to include a 90° angle.Answers: 1)
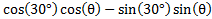 2)
2) 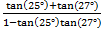 or
or 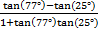 3)
3) 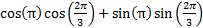 4)
4) 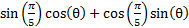 5)
5) 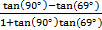
|
Related Links: Math Fractions Factors |
