Using the Law of Sines to Find an Unknown Side
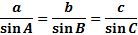
Remember that a stands for the side across from angle A, b is the side across from angle B, and c is the side across from angle C.
Once again, this law is extremely useful because it works for any triangle, not just a right triangle.
In a previous lesson we looked at how to use the Law of Sines to find an unknown angle. In this lesson, we'll use it to find an unknown side.
To find an unknown side using the Law of Sines:
1. Substitute the known values into the formula.
2. Remove the fraction that is unhelpful.
3. Solve the remaining equation.
2. Remove the fraction that is unhelpful.
3. Solve the remaining equation.
To further study this law, let's examine the following triangle:
If we want to solve this triangle, we must find length of side a, the length of side c, and the measure of angle C. Let's look at each of those:
1. Find the measure of side a.
2. Find the measure of angle C.
3. Find the measure of side c.
Practice:Use the Law of Sines to find the given piece of information for each triangle shown. Refer to the pictures below and round your answer to the nearest tenth if necessary. (Note, pictures may not be to scale.)
First we'll substitute the information we have into the Law of Sines:
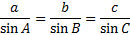
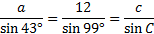
As you can see, we have enough information to find side a, but the last fraction is not helpful at all. Let's rewrite the law without it:
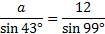
Next we must solve the equation. Since sin 43° is being divided by a, we'll multiply both sides by that.
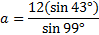And we'll use our calculator to find the length of side a:
a ≈8.3 m.
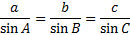
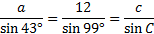
As you can see, we have enough information to find side a, but the last fraction is not helpful at all. Let's rewrite the law without it:
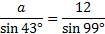
Next we must solve the equation. Since sin 43° is being divided by a, we'll multiply both sides by that.
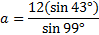
a ≈8.3 m.
2. Find the measure of angle C.
We cannot use the Law of Sines to find the measure of angle C, but we can use the fact that the three angles must add up to 180° .
180 - 99 - 43 = 38
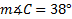
180 - 99 - 43 = 38
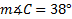
3. Find the measure of side c.
We'll use the Law of Sines again. Let's start by substituting:
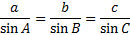
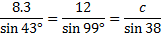
We can either eliminate the 1st or 2nd fraction. Since we calculated the value of a ourselves and had to round, this value is less reliable. Therefore, let's eliminate the 1st fraction. (By the way, if you eliminate the 2nd fraction instead, you should get approximately the same answer - assuming you calculated a correctly.)
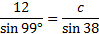
Next we must solve the equation. Since sin 38° is being divided by c, we'll multiply both sides by that.
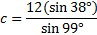
And we'll use our calculator to find the length of side c:
c ≈7.5 m.
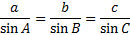
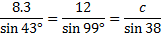
We can either eliminate the 1st or 2nd fraction. Since we calculated the value of a ourselves and had to round, this value is less reliable. Therefore, let's eliminate the 1st fraction. (By the way, if you eliminate the 2nd fraction instead, you should get approximately the same answer - assuming you calculated a correctly.)
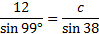
Next we must solve the equation. Since sin 38° is being divided by c, we'll multiply both sides by that.
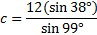
And we'll use our calculator to find the length of side c:
c ≈7.5 m.
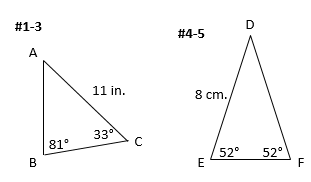
Practice:Use the Law of Sines to find the given piece of information for each triangle shown. Refer to the pictures below and round your answer to the nearest tenth if necessary. (Note, pictures may not be to scale.)
1. Find the length of side c.
2. Find the measure of angle A.
3. Find the length of side a.
4. Find the length of side e.
5. Find the length of side d.
2. Find the measure of angle A.
3. Find the length of side a.
4. Find the length of side e.
5. Find the length of side d.
Answers: 1) 6.1 in. 2) 66° 3) 10.2 in. 4) 8 cm. 5) 9.9 cm.
|
Related Links: Math Fractions Factors |