Writing the Equation of an Ellipse
Remember the patterns for an ellipse:
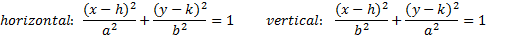
(h, k) is the center point, a is the distance from the center to the end of the major axis, and b is the distance from the center to the end of the minor axis.
Remember that if the ellipse is horizontal, the larger number will go under the x. If it is vertical, the larger number will go under the y.
Let's look at a couple examples:
1. Find the equation of this ellipse:
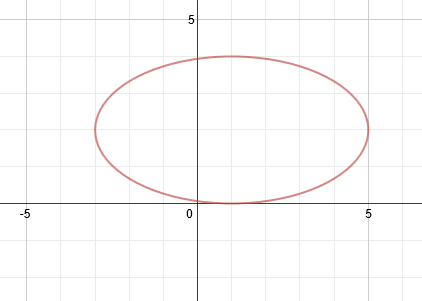
First, let's mark the center point on the graph to make things more clear.
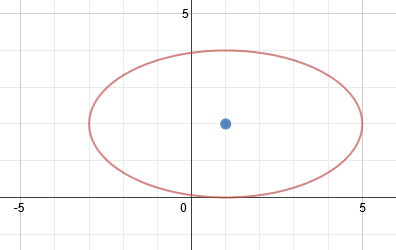
The center point is (1, 2). We can also tell that the ellipse is horizontal. Let's identify a and b. Counting the spaces from the center to the ellipse lengthwise, we can tell that a = 4. Then counting up, we know that b = 2.
Now we need to substitute this information into the pattern. Since it's a horizontal ellipse, we know that the larger number (a) needs to go underneath the x.
Now we need to substitute this information into the pattern. Since it's a horizontal ellipse, we know that the larger number (a) needs to go underneath the x.
Center point: (1, 2) a = 4, b = 2
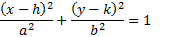
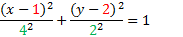
To finish, we just need to simplify:
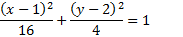
2. Find the equation of this ellipse:
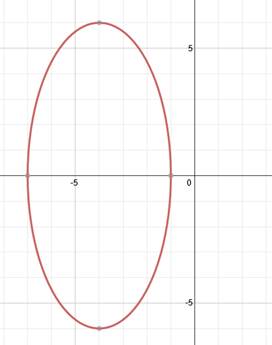
Let's mark the center point again to make things more clear.
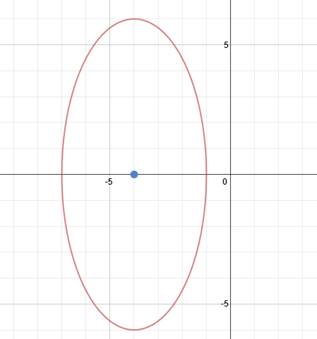
The center point is (-4, 0). We can also tell that the ellipse is vertical. Let's identify a and b. Counting the spaces from the center to the ellipse vertically, we can tell that a = 6. Then counting to the right, we know that b = 3.
Now we need to substitute this information into the pattern. Since it's a vertical ellipse, we know that the larger number (a) needs to go underneath the y.
Now we need to substitute this information into the pattern. Since it's a vertical ellipse, we know that the larger number (a) needs to go underneath the y.
Center point: (-4, 0) a = 6, b = 3
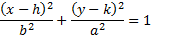
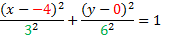
To finish, we just need to simplify:
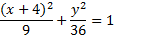
Practice: Find the equation of each ellipse.
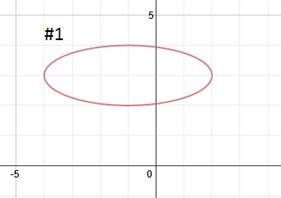
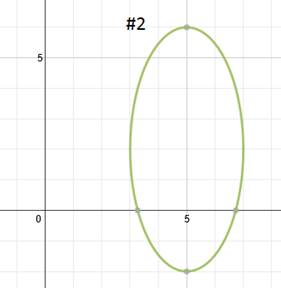
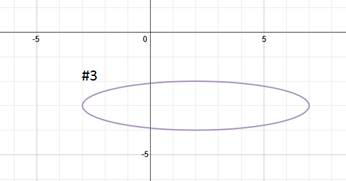
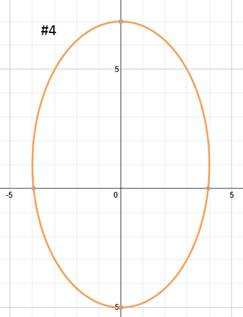
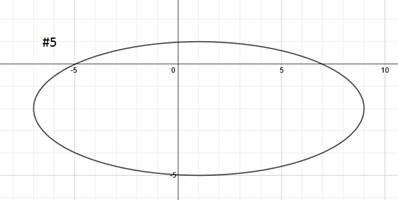
Answers:
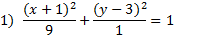
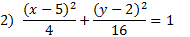
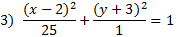
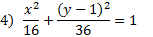
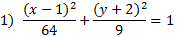
|
Related Links: Math Fractions Factors |
