Area of a Circle
Keep in mind that pi is an irrational number. That means that it cannot be written as a fraction. As a decimal, it will be a number that never ends and never repeats. So when we calculate the area, we will either need to leave the answer in terms of pi or round the answer. Here are some examples:
Determine the area of the following circles.
1.)
2.)
3.) The area of a circle is 49∏ ft.2. Determine the radius and the diameter.
Work backwards to get the radius.
A = ∏r2
49∏ = ∏r2
The pi symbol cancels out from both sides.49 = r2
Take the square root of 49 to determine r.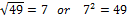
7 ft. = r
Double the radius to determine the diameter.14 ft. = d
Let's Review
To determine the area of a circle there are just two steps.
1.) Square the radius. This means multiply the number by itself.
2.) Multiply the product times pi.
2.) Multiply the product times pi.
a. If you are leaving the answer in terms of pi, then you can just leave the pi symbol in the answer.
b. If you are not leaving the answer in terms of pi, be sure to check to see what place you need to round the answer. It might be the nearest whole, tenth, hundredth, thousandth, etc.
c. Because this is an area, label the solution with square units.
b. If you are not leaving the answer in terms of pi, be sure to check to see what place you need to round the answer. It might be the nearest whole, tenth, hundredth, thousandth, etc.
c. Because this is an area, label the solution with square units.
|
Related Links: Math Geometry Area of a Circle Circumference of a Circle |