Area of Rectangles and Squares
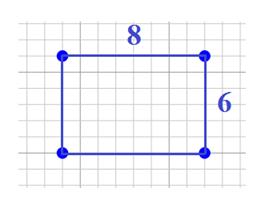
If you took the time to count all the squares, you should see that there are 48. That means that the area of the rectangle, or the space that covers the rectangle, is 48 square units.
However, counting the squares is not a very efficient way to determine the area. There is a better way.
A = lw
A = 8 units x 6 units
A = 48 square units or 48 units2
However, counting the squares is not a very efficient way to determine the area. There is a better way.
A = lw
A = 8 units x 6 units
A = 48 square units or 48 units2

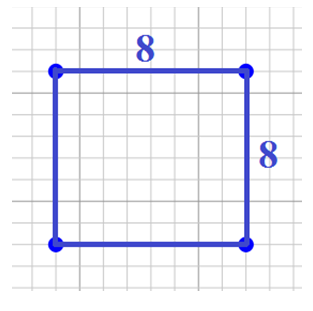
A special type of rectangle, called a square, has four equal sides.
Because the sides are equal, when we multiply the length and width, we get a number times itself, or a number squared.
So for squares, we can simplify the formula and
use A = s2.
Here are some more examples:
Let's Review
To determine the area of a rectangle, we must multiply the length and width.
We use the formula A = lw. If we are given the area and one side, we can work backwards by dividing to determine the length of the other side.
To determine the area of a square, we could use the rectangle formula, or we can use a special formula: A = s2. If we are given the area of a square, we can work backwards, or take the square root to determine the side length.
use A = s2.
A = s2
A = (8 units)2
A = 64 units2
A = (8 units)2
A = 64 units2

Here are some more examples:
1.) Calculate the area of a rectangle with a length of 4 and a width of 9 units.
Solution: A = lw
A = (4 units)(9 units)
A = 36 units2
A = (4 units)(9 units)
A = 36 units2
2.) Determine the area of the rectangle
Solution: A = lw
A = (3 in)(18 in)
A = 54 in2
A = (3 in)(18 in)
A = 54 in2

3.) The area of a rectangle is 30 cm2 and the length is 6 cm. What is the width of the rectangle?
Solution: Because we are given the area, work backwards by dividing.
A = lw
30 cm2 = (6 cm)w
30 cm2 ÷ 6 cm = w
5 cm = w
A = lw
30 cm2 = (6 cm)w
30 cm2 ÷ 6 cm = w
5 cm = w
4.) Determine the area of a square with a side length 10 cm.
A = s2
A = (10 cm)2
A = 100 cm2
A = (10 cm)2
A = 100 cm2
5.) Determine the area of the shape shown.
A = s2
A = (7 mm)2
A = 49 mm2
A = (7 mm)2
A = 49 mm2

6.) The area of a square is 144 in2. What is the length of each side?
Solution: Because we are given the area, work backwards by taking the square root.
A = s2
144 in2 = s2
√144 in2 = √s2
12 in = s
A = s2
144 in2 = s2
√144 in2 = √s2
12 in = s
7.) The area of a square is 225 cm2. What is the perimeter?
Solution: to determine the perimeter, we must first determine the side length. Then use the side length to determine the perimeter.
A = s2 P = 4s
225 cm2 = s2 P = 4(15 cm)
√225 cm2 = √s2 P = 60 cm
15 cm = s
A = s2 P = 4s
225 cm2 = s2 P = 4(15 cm)
√225 cm2 = √s2 P = 60 cm
15 cm = s
Let's Review
To determine the area of a rectangle, we must multiply the length and width.
We use the formula A = lw. If we are given the area and one side, we can work backwards by dividing to determine the length of the other side.
To determine the area of a square, we could use the rectangle formula, or we can use a special formula: A = s2. If we are given the area of a square, we can work backwards, or take the square root to determine the side length.
|
Related Links: Math Geometry Perimeter game for square and rectangle Area of Rectangle Perimeter of Rectangle Area of a Square Perimeter of Square |
