Missing Angles in Triangles Knowing that a triangle contains 180° makes calculating the measure of a missing angle much simpler.

Let's take a look at some examples.

Example #1:

Determine the measure of angle x.



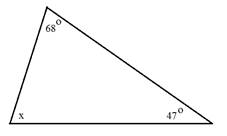
Step 1: Add together the known angles.

68° + 47° = 115°

Step 2: Subtract the sum from 180°.

180° - 115° = 65°

The measure of angle x is 65°.



Example #2:

Determine the measure of angle y.



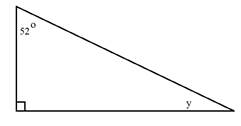
Notice that this triangle has a right angle in the bottom left corner. This angle measures 90°.

Step 1: Add the measure of the given angles together.

52° + 90° = 142°

Step 2: Subtract the sum from 180°.

180° - 142° = 38°

The third angle measures 38°.



Example 3:

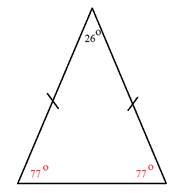
Determine the measure of angle m.



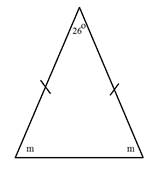
Notice that this triangle is isosceles. That means that not only are two of the sides equal but two of the angles are also equal. The solution to this problem will be slightly different than the solution to the others.

Step 1: Subtract the know angle from 180°.

180° - 26° = 154°

Step 2: Divide the difference by 2 to get the measure of each angle.

154° ÷ 2 = 77°

Each angle m measures 77°.



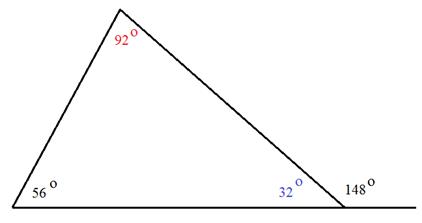
Example 4:

Determine the measure of angle h.



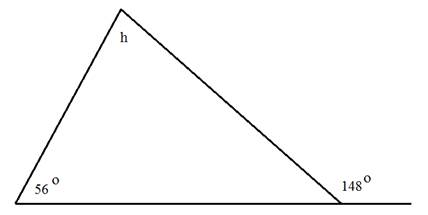
Notice that this triangle gives an angle outside of the triangle. There are a couple of different ways you can use this information to determine the measure of angle h.

Here is one method:

Step 1: Determine the measure of the angle adjacent to 148°.

The two angles make a straight line and therefore have a sum of 180°.

180° - 148° = 32°



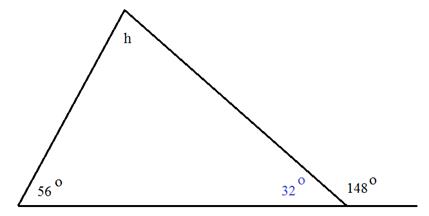
Step 2: Add together the two known angles inside the triangle.

56° + 32° = 88°

Step 3: Subtract the sum from 180°.

180° - 88° = 92°

The measure of angle h is 92°.



Let's Review

To determine to measure of the unknown angle, be sure to use the total sum of 180°. If two angles are given, add them together and then subtract from 180°. If two angles are the same and unknown, subtract the known angle from 180° and then divide by 2.

Related Links: Math Geometry Interior Angles of Triangle