Direction Angles of Vectors

Figure 1 shows a unit vector u that makes an angle θ with the positive x-axis. The angle θ is called the directional angle of vector u.

The terminal point of vector u lies on a unit circle and thus u can be denoted by:

$u = 〈 x, y 〉 = 〈 \cos θ, \sin θ 〉 = (\cos θ) i + (\sin θ) j$

Any vector that makes an angle θ with the positive x-axis can be written as the unit vector times the magnitude of the vector.

$v = ∥ v ∥ (\cos θ) i + ∥ v ∥ (\sin θ) j$

$v = a i + b j$

Therefore the direction angle of θ of any vector can be calculated as follows:

DIRECTIONAL ANGLE:

$tan θ = \frac{s i n θ}{\cos θ} = \frac{∥ v ∥ s i n θ}{∥ v ∥ \cos θ} = \frac{b}{a}$

Let's look at some examples.

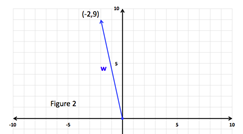
To work these examples requires the use of various vector rules. If you are not familiar with a rule go to the associated topic for a review.

Example 1:Find the direction angle of w = -2i + 9j.

Step 1: Identify the values for a and b and calculate θ.

$t a n θ = \frac{b}{a}$

a = -2, b = 9

$\tan θ = \frac{b}{a} = \frac{9}{- 2}$

$θ = \tan^{- 1} | \frac{9}{- 2} |$

$θ \approx 78 °$

Step 2: Determine the Quadrant the vector lies in.

Because the vector terminus is (-2, 9), it will fall in quadrant II and so will θ.

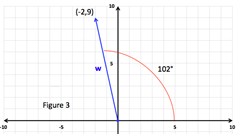
Step 3: Make any necessary adjustments to find the directional angle θ from the positive x-axis.

Since the reference angle is 78°, the directional angle from the positive x-axis is 180° - 78° = 102°.

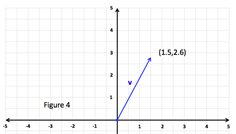
Example 2:Find the direction angle of $v = 3 (\cos 60 ° i + \sin 60 ° j)$ .

Step 1: Simplify vector v using scalar multiplication. $k v = k v_{1}, v_{2} = k v_{1}, k v_{2} \to S c a l a r M u l t i p l i c a t i o n$	$v = 3 (\cos 60 ° i + \sin 60 ° j)$ $v = 3 \cdot \cos 60 ° i + 3 \cdot \sin 60 ° j$ $v = 3 \cdot \frac{1}{2} i + 3 \cdot \frac{\sqrt{3}}{2} j$ $v = \frac{3}{2} i + \frac{3 \sqrt{3}}{2}$
Step 2: Identify the values for a and b and calculate θ.	$a = \frac{3}{2}, b = \frac{3 \sqrt{3}}{2}$ $\tan θ = \frac{b}{a} = \frac{\frac{3 \sqrt{3}}{2}}{\frac{3}{2}} = \frac{3 \sqrt{3}}{2} \cdot \frac{2}{3} = \sqrt{3}$ $θ = \tan^{- 1} \| \sqrt{3} \|$ $θ = 60 °$
Step 3: Determine the Quadrant of the vector lies in.	Because the vector terminus is $(\frac{3}{2}, \frac{3 \sqrt{3}}{2}) = (1.5, 2.6)$ and both components are positive the vector will fall in quadrant I and so will θ.
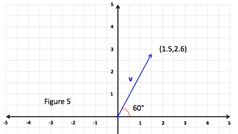
Step 4: Make any necessary adjustments to find the directional angle θ from the positive x-axis.	Since the reference angle is 60°, the directional angle from the positive x-axis is 60° - 0° = 60°.

Related Links:
Math
algebra
The Dot Product
Angle between Two Vectors
Pre Calculus

To link to this Direction Angles of Vectors page, copy the following code to your site:

<a href="https://www.softschools.com/math/pre_calculus/direction_angles_of_vectors/">Direction Angles of Vectors</a>

Direction Angles of Vectors

More Topics

Educational Videos