GCF - Greatest Common Factor

Remember that factors are the numbers we multiply together to get another number

Example: 2 x 9 = 18

2 and 9 are factors of 18.

When we have two or more given numbers, we can find the largest factor that both numbers have in common. This is called the GCF or the Greatest Common Factor.

There are several different methods that can be used to find the GCF. Let's take a look at some of the methods.

Method 1: List out the factors.

Example: Find the GCF of 64 and 96.

Step 1: List the factors of each number.

64: 1, 2, 4, 8, 16, 32, 64

96: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96

Step 2: Look for factors that both lists have in common.

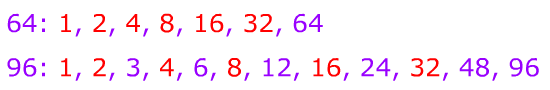
Step 3: Pick out the largest factor that both lists have in common and call this the GCF.

Therefore, the GCF of 64 and 96 is 32.

Method 2: Upside Down Division

Find the GCF of 280 and 144.

Step 1: Place the numbers inside an upside down division bar.

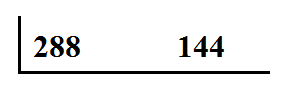
Step 2:Now, we need to divide both numbers by a common factor. Because both of the numbers are even, we could start with 2.The answer goes underneath the bar.

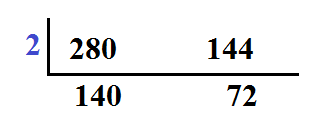
Step 3: We will continue to divide until we have two numbers that are relatively prime. Remember that relatively prime means two numbers that do not have any common factors other than 1.

35 and 18 are relatively prime.

Step 4: Now we take all of the factors on the side and multiply them together.

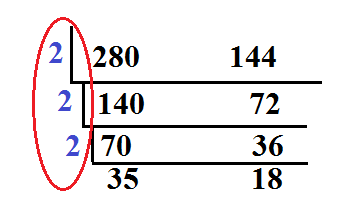
2 x 2 x 2 = 8

This means that the GCF of 280 and 144 is 8.

Method 3: Prime Factorization

We can also use the prime factorization of two numbers to help us get the GCF.

Example: Find the GCF of 150 and 225.

Step 1: Start by making factor trees for each of the numbers.

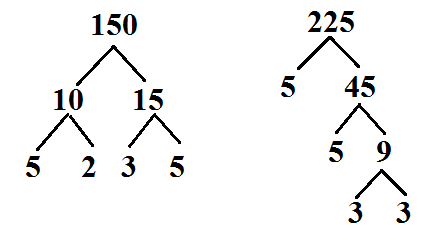
Step 2: List out the prime factorization for each number.

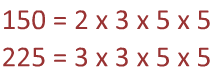
Step 3: Now circle the prime factors that each number has in common.

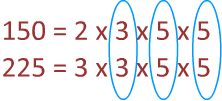
Step 4: Next, multiply the circled numbers together. 3 x 5 x 5 = 75

This tells us that the GCF of 150 and 225 is 75.

You might wonder why the GCF is important. Not only is the GCF extremely important when working with fractions, but is can also be used when applying the distributive property or when solving word problems. Let's take a look at an example of a word problem that uses GCF.

Example: Maria has 160 pieces of chocolate candy and 144 pieces of fruity candy. She wants to give each child the same amount of candy so that no one feels left out. What is the greatest number of children she can give candy?

Step 1: We know that this is a GCF question because Maria is breaking the candy into groups and the problem using the key word 'greatest'. First, we must choose a method. Let's use upside down division.

Step 2: Solve for the GCF.

Step 3: Use the GCF to answer the question.

From the upside down division, we can see that she could give candy to 16 children. The bottom of the upside down division gives us even more information.

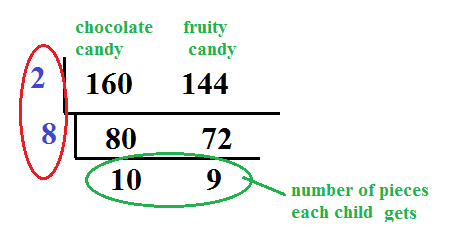
From the upside down division, we can see that each child would get 10 pieces of chocolate candy and 9 pieces of fruity candy. No candy will be left over and each child will get the same amount.

Let's Review:

The GCF is the largest factor that two or more numbers have in common. You can find it by listing the factors, using upside down division or by using the prime factorization. GCF is helpful in problem solving as well. When we see key words like largest, greatest and most combined with questions about breaking things into groups we know that we are solving a GCF question.

GCF - Greatest Common Factor

More Topics

Educational Videos