Multiply and dividing with integers is much like multiplying and dividing with whole numbers. You just have to be careful of the signs.

Examples:2 x 3 = 6

Multiplying is really just showing repeated adding. So, we need to add 2 three times. 2 + 2 + 2 = 6

How would this look on a number line?



Now, let's take a look at how this works with negatives.

Examples:-2 x 3 = -6

This one is asking us to add -2 three times. That means that we would have -2 + -2 + -2 = -6.

We can take a look at this on the number line as well.



What if there were two negatives?

Examples:-2 x -3 = 6

This example says that we should add -2 negative 3 times. How do you add something negative times?

Well, we can also think of the negative symbol as meaning "the opposite". So if we are going to add - 2 the opposite of 3 times, we will move in the opposite direction on the number line. We had moved to the left, so now we move to the right.



Let's take what we have seen in the examples and write some simpler rules.

Rule #1:If the signs are the same, the answer is positive.

Examples:

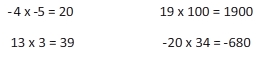
Rule #2:If the signs are different, the answer is negative.

Examples:

The great news is that the rules for dividing integers are the same as the rules for multiplying integers.

Remember that dividing is the opposite of multiplying. So we can use the same rules to solve.

Rule #1:If the signs are the same, the answer is positive.

Examples:

Rule #2:If the signs are different, the answer is negative.

Examples:

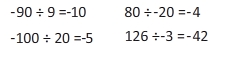
When trying to remember the rule, you can say to yourself, "Are my signs the same?"

If you answer oooooo, then the answer is egative.

If you answer Yes, then the answer is Positive. Otherwise, the multiplying and dividing is the same as with whole numbers.