Sometimes, simplifying a fraction, or reducing the fraction, can help give more information about a problem.

When we simplify a fraction, we are writing another fraction that is equal to the original; it is just written in another way.


To get a visual idea of what this means, look at the example below of



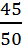
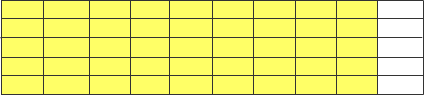
We could change the way we view this by just getting rid of some of the lines.



Here we can see that 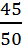is the same as .

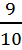Nine-tenths is an easier way to think about the information. It is also easier to convert to a percent or work with in other ways.

However, drawing a diagram can be a tedious way to simplify a fraction. There are other methods.

Example: Simplify

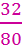
In order to simplify, we need to find common factors. Because both of the numbers are even, we could start by dividing by 2.



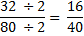
Now you might notice that 4 divides into both 16 and 40 without a remainder, so we can divide again.



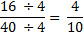
We check our numbers again, and can see that 4 and 10 still have another common factor of 2. So we divide again.



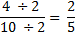
Finally, we have simplified the fraction to lowest terms. We know this because 2 and 5 are relatively prime, or they have no other common factors besides 1. This means that the fraction cannot be reduced again.

If you don't like dividing this way, you can also use the upside down division.

Example: Simplify the fraction

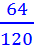
Place both numbers in the upside down division.



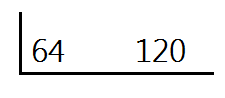
Next, we will divide both numbers by a common factor. It doesn't matter what number you start with, as long as it is a factor of both numbers. If you have trouble coming up with a factor and both numbers are even, you can always start by dividing by 2.



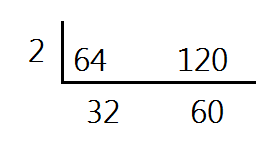
32 and 60 still have common factors, so we will repeat the steps until there are no more common factors.



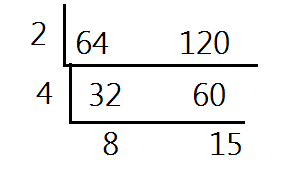
The numbers at the bottom are relatively prime because they have no other common factors besides 1. At this point, the fraction has been simplified to lowest terms. The numbers at the bottom form the new fraction. The first number becomes the numerator and the second number becomes the denominator.



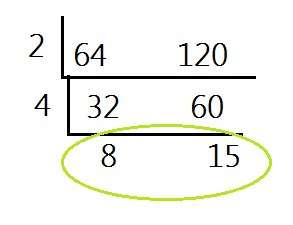
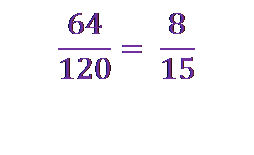
So the fraction 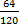reduced to lowest terms is equal to .

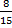Let's Review: Fractions can be written in many forms. When we reduce or simplify the fraction, we are writing a fraction in an equivalent form that may be easier to work with. In order to simplify, we divide both the numerator and the denominator by a common factor. The fraction is in lowest terms when there is no longer a common factor other than 1.