We often think of subtraction as "taking away." However, when we work with integers, subtraction can look quite the opposite.

Subtraction can be done by adding the opposite. Let's take a look at a simple example to see how the two are related.

Example: 5 - 3

We can write this as 5 + (-3). Both 5 -3 and 5 + (-3) = 2. When we subtract a positive number, we move to the left on the number line. This is the same thing that happens when we add a negative number.



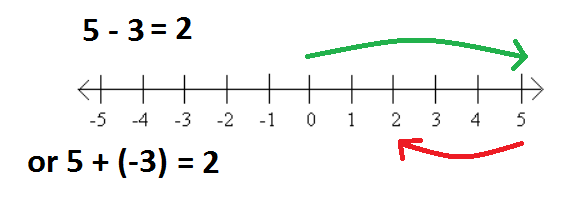
We can use this to help us subtract negatives.

Example: 6 - (-9)

Just like in the example above, we can change this question to adding the opposite.

6 - (-9) becomes 6 + 9 = 15. You might be wondering how we can subtract and end up with a larger number than we started with. Let's look at the number line. When we subtracted a positive number we moved to the left. So when we subtract a negative number we need to move to the right.



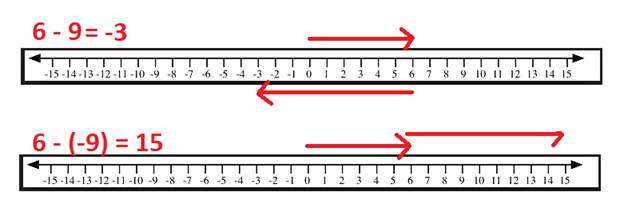
In the number line, you can see that when a negative number is being subtracted, we actually move towards the larger numbers on the number line. Drawing out the number line can be a little tedious every time you go to subtract. So we can use a little saying to help us remember how it works.

Keep Change Change or KCC

This means to KEEP the first number the same. CHANGE the subtracting to adding. Then CHANGE the sign of the second number.

Check it out:

17 - (-5)

Keep the 17. Change the minus to a plus. Change the -5 to a positive 5.



Here is another:

-18 - 5

Keep the -18. Change the minus to a plus. Change the positive 5 to a -5.



One last example:

-23 - (-11)

Keep the -23. Change the minus to a plus. Change the negative 11 to a positive 11.



From these examples, we can see that subtracting with integers is the same as adding the opposite. We can solve using a number line or by using the saying "Keep, Change, Change" to help us solve. It is important to remember that we can subtract a negative and end up with a larger number than we started with.