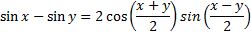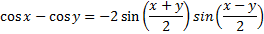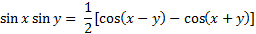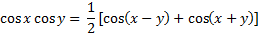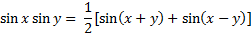The process of converting products into sums and sums into products can be a very useful tool in integration. It is also the difference in finding an easy solution versus no solution at all. The product-sum identity and the sum-product identity can be derived from the sum and difference identities.

Sum-Product Identities

Alternate forms of the sum-product identities are the product-sum identities.

Product-Sum Identities

Example 1: Express the product cos(3x)sin(2x) as a sum of trigonometric functions.

Step 1: Notice that the problem is the product of cosine and sine, therefore use the product- sum identity

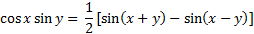
Step 2: Using substitution let x = 3x and y = 2x

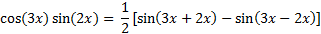
Step 3: Simplify

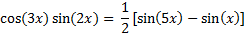
Example 2: Express the sum cos(5x) + cos(7x) as a product trigonometric functions

Step 1: Notice that it is a sum of cosine and cosine, therefore use the sum-product identity:

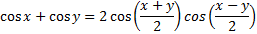
Step 2: Using substitution let x = 5x and y = 7x

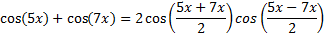
Step 3: Simplify

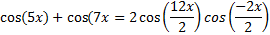
Step 4: Use the even/odd function rule cos(-x) = cos (x) to replace 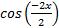with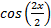

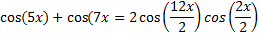
Example 3: Find the exact value of sin 75° + sin 15°.

Step 1: Notice that it is a sum of sine and sine, therefore use the sum-product identity:

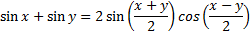
Step 2: Using substitution let x = 75 and y = 15

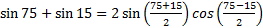
Step 3: Simplify

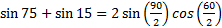
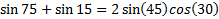
Step 4: Substitute the familiar values of sin 45 = 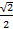and cos 30 = 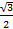into the equation and simplify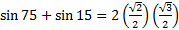

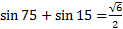
Using the sum-product and the product- sum identities can make it easier to rewrite trigonometric identities in order to evaluate functions.

Related Links: Math Trigonometry Double Angle Identities Half Angle formulas