Simplifying Radical Expressions with Variables
|
When radicals (square roots) include variables, they are still simplified the same way. We just have to work with variables as well as numbers
1) Factor the radicand (the numbers/variables inside the square root). Factor the number into its prime factors and expand the variable(s). 2) Bring any factor listed twice in the radicand to the outside. Examples:
1) 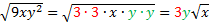 Since there was a pair of 3's and a pair of y's, we brought the 3 and the y outside, but the x stayed inside since it was not a pair. 2) 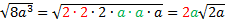 3) 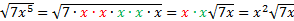 Notice that there were two pairs of x's, so we were able to bring two to the outside. The last x, however, was not part of a pair and thus stayed inside. Practice: Simplify
1) 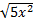 2) 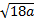 3) 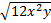 4) 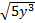 5) 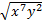 Answers: 1) 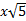 2) 2)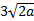 3) 3)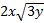 4) 4)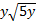 5) 5)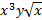 |
|
Related Links: Math Algebra Factors |
