Finding Slant Asymptotes of Rational Functions
To find the slant asymptote you must divide the numerator by the denominator using either long division or synthetic division.
Examples: Find the slant (oblique) asymptote.
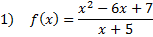
Since the polynomial in the numerator is a higher degree (2nd) than the denominator (1st), we know we have a slant asymptote. To find it, we must divide the numerator by the denominator. We can use long division to do that:
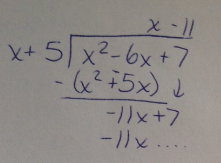
Notice that we don't need to finish the long division problem to find the remainder. We only need the terms that will make up the equation of the line. The slant asymptote is
y = x - 11.
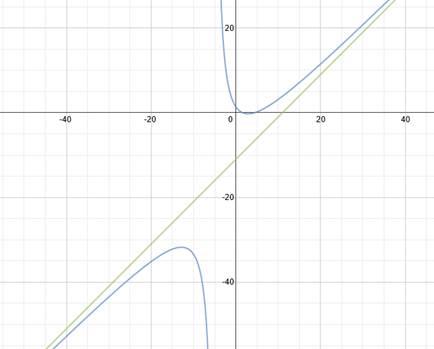
As you can see in this graph of the function, the curve approaches the slant asymptote y = x - 11 but never crosses it:
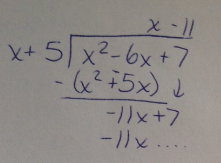
Notice that we don't need to finish the long division problem to find the remainder. We only need the terms that will make up the equation of the line. The slant asymptote is
y = x - 11.
As you can see in this graph of the function, the curve approaches the slant asymptote y = x - 11 but never crosses it:

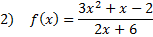
Since the polynomial in the numerator is a higher degree (2nd) than the denominator (1st), we know we have a slant asymptote. To find it, we must divide the numerator by the denominator. We can use long division to do that:
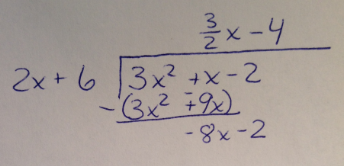
Once again, we don't need to finish the long division problem to find the remainder. We only need the terms that will make up the equation of the line.
The slant asymptote is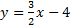 .
.
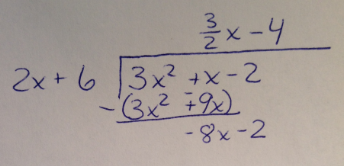
Once again, we don't need to finish the long division problem to find the remainder. We only need the terms that will make up the equation of the line.
The slant asymptote is
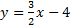 .
.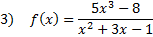
Since the polynomial in the numerator is a higher degree (3rd) than the denominator (2nd), we know we have a slant asymptote. To find it, we must divide the numerator by the denominator. We can use long division to do that:
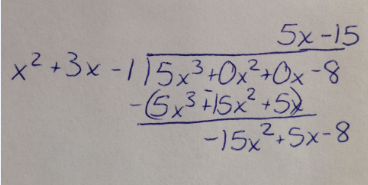
Once again, we don't need to finish the long division problem to find the remainder. We only need the terms that will make up the equation of the line. The slant asymptote is
y = 5x - 15.
Practice: Find the slant asymptote of each rational function: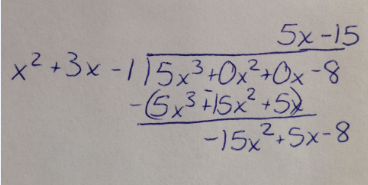
Once again, we don't need to finish the long division problem to find the remainder. We only need the terms that will make up the equation of the line. The slant asymptote is
y = 5x - 15.
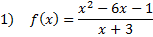
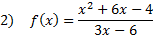
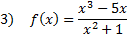
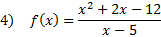
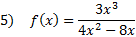
Answers: 1) y = x - 9 2)
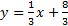 3) y = x 4) y = x + 7 5)
3) y = x 4) y = x + 7 5) 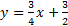
|
Related Links: Math Fractions Factors |
