Finding the Foci of an Ellipse
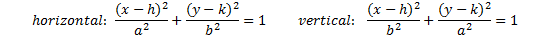
Each ellipse has two foci (plural of focus) as shown in the picture here:
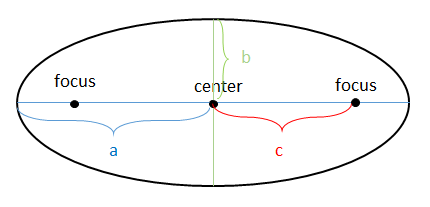
As you can see, c is the distance from the center to a focus.
We can find the value of c by using the formula c2 = a2 - b2. Notice that this formula has a negative sign, not a positive sign like the formula for a hyperbola.
We can easily find c by substituting in a and b and solving. That, in turn, gives us the location of our foci.
Let's find c and graph the foci for a couple ellipses:
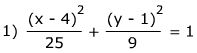
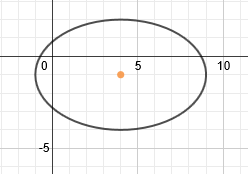
This ellipse has already been graphed and its center point is marked:
We need to use the formula c2 = a2 - b2 to find c. Now, we could find a and b and then substitute, but remember that in the pattern, the denominators are a2and b2, so we can substitute those right into the formula:
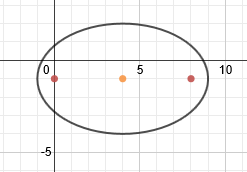

We need to use the formula c2 = a2 - b2 to find c. Now, we could find a and b and then substitute, but remember that in the pattern, the denominators are a2and b2, so we can substitute those right into the formula:
c2 = a2 - b2
c2 = 25 - 9
c2 = 16 We'll need to take the square root.
c = 4
We can plot the foci by counting 4 spaces from the center. Since the ellipse is horizontal, we will count 4 spaces left and right and plot the foci there.c2 = 25 - 9
c2 = 16 We'll need to take the square root.
c = 4

2) Find the equation of this ellipse:
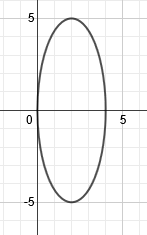
time we do not have the equation, but we can still find the foci. Let's start by marking the center point:
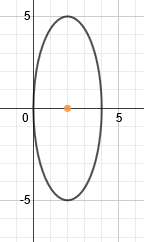
Looking at this ellipse, we can determine that a = 5 (because that is the distance from the center to the ellipse along the major axis) and b = 2 (because that is the distance from the center to the ellipse along the minor axis).
We need to use the formula c2=a2-b2 to find c. We will substitute these values in and solve.
c2 = a2 - b2
c2 = 52 - 22
c2 = 25 - 4
c2 = 21 We'll need to take the square root.
c ≈ 4.6
We can plot the foci by counting about 4.6 spaces from the center. We'll have to estimate somewhat, but we can be fairly accurate.Since the hyperbola is vertical, we will count 4.6 spaces up and down and plot the foci there.
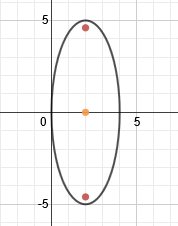
Practice: 
time we do not have the equation, but we can still find the foci. Let's start by marking the center point:

Looking at this ellipse, we can determine that a = 5 (because that is the distance from the center to the ellipse along the major axis) and b = 2 (because that is the distance from the center to the ellipse along the minor axis).
We need to use the formula c2=a2-b2 to find c. We will substitute these values in and solve.
c2 = a2 - b2
c2 = 52 - 22
c2 = 25 - 4
c2 = 21 We'll need to take the square root.
c ≈ 4.6
We can plot the foci by counting about 4.6 spaces from the center. We'll have to estimate somewhat, but we can be fairly accurate.Since the hyperbola is vertical, we will count 4.6 spaces up and down and plot the foci there.

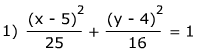
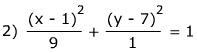
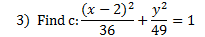
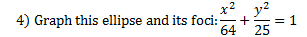
1) c = 3 2) c ≈ 2.8 3) c ≈ 3.6
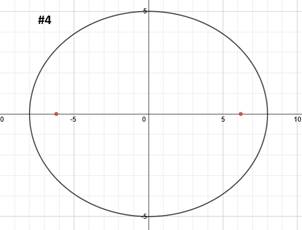
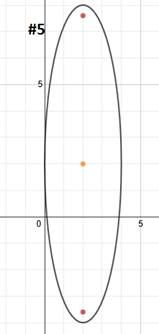
|
Related Links: Math Fractions Factors |
