Rolle's Theorem
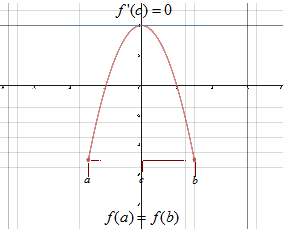
Rolle's Theorem states that under certain conditions an extreme value is guaranteed to lie in the interior of the closed interval.
ROLLE'S THEOREM
Conditions:
2. The function f must be differentiable on the open interval (a, b).
3. f(a) = f(b)
Let's use this theorem in a couple examples.
|
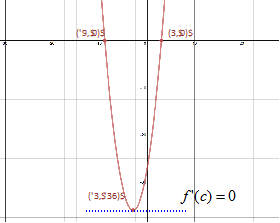
Step 1: Find the x-intercepts or zeros of the function. |
x2 + 6x - 27 = 0 Original (x + 9)(x - 3) = 0 Factor Set to zero & solve Set to zero & solve |
|
Step 2: Find the first derivative of the function. |
|
|
Step 3: Solve for . |
0 = 2x + 6 -3 = x Solve |
|
Step 4: Compare x-intercepts to the value in Step 3 when . and -3 falls between -9 and 3, therefore there is a minimum point at (-3, -36).
|
|
|
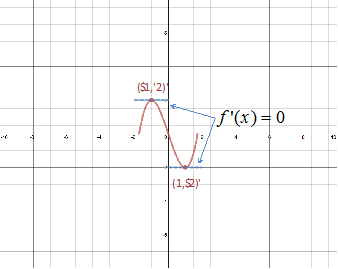
Step 1: Find the first derivative of the function. |
f(x) = x3 - 3x
|
|
Step 2: Set the first derivative equal to zero and solve. |
First derivative 0 = 3x2 - 3 Set 0 = 3(x2 - 1) Factor out a 3 0 = 3(x - 1)(x + 1) Factor the quad. Solve for x Solve for x |
|
Step 3: Substitute the x-coordinates found in Step 2 into the function to determine the corresponding y-coordinates. |
f(1) = -2 f(-1) = 2 |
|
Step 4: Name the coordinates The coordinates of the two points where are (1, -2) and (-1, 2).
|
|
|
Related Links: Math algebra The Mean Value Theorem Limits: Introduction and One-Sided Limits Calculus Topics |
To link to this Rolle's Theorem page, copy the following code to your site: