Solving Basic Logarithmic Equations
1. Get the logarithm by itself on one side of the equation.
2. Determine the base of the logarithm.
3. Raise both sides of the equation to be a power of that base.
4. Simplify and solve.
Examples:
1)
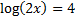
The logarithm is already by itself. The base of the log is 10, so we must raise both sides of the equation to be powers of 10:
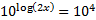
On the left hand side, the 10 and log cancel, leaving just 2x.
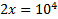
2x = 10,000
x = 5,000
We can check this answer by substituting it back in for x.
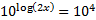
On the left hand side, the 10 and log cancel, leaving just 2x.
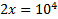
2x = 10,000
x = 5,000
We can check this answer by substituting it back in for x.
2)
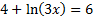
First, we'll move the 4 to the other side to get the natural log by itself:
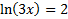
The base of the log is e, so we must raise both sides of the equation to be powers of e:
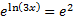
On the left hand side, the e and ln cancel, leaving just 3x.
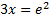
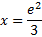
This is the exact answer, but we can find an estimation using our calculator:
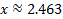
We can check this answer by substituting it back in for x.
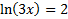
The base of the log is e, so we must raise both sides of the equation to be powers of e:
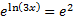
On the left hand side, the e and ln cancel, leaving just 3x.
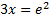
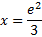
This is the exact answer, but we can find an estimation using our calculator:
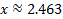
We can check this answer by substituting it back in for x.
3)
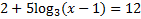
First we must get the log by itself by moving the 2 and the 5:
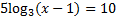
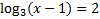
The base of the log is 3, so we must raise both sides of the equation to be powers of 3:
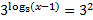
On the left hand side, the 3 and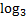
cancel, leaving just x - 1.
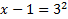
x - 1 = 9
x = 10
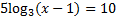
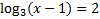
The base of the log is 3, so we must raise both sides of the equation to be powers of 3:
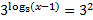
On the left hand side, the 3 and
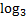cancel, leaving just x - 1.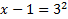x - 1 = 9
x = 10
Practice: Solve each logarithmic equation. If necessary, round the answer to the nearest thousandth.
1)
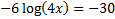
2)
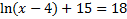
3)
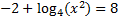
4)
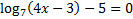
5)
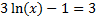
Answers: 1) 25,000 2) 24.086 3) ±1024 4) 4202.5 5) 3.794
|
Related Links: Math Fractions Factors |