Understanding Hyperbolas
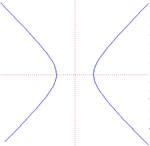
Let's look at some of the key parts of a hyperbola. In this example, we have a vertical hyperbola.
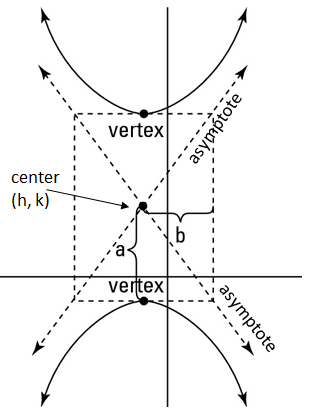
Notice that (h, k) is the center of the entire hyperbola but does not actually fall on the hyperbola itself. Each hyperbola has a vertex and two asymptotes guide how wide or how narrow the curve is.
There are two patterns for hyperbolas.
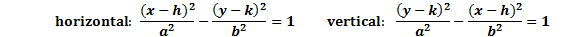
By examining the equation, we can determine the following:
1. If it is vertical or horizontal. If the x term is positive, the parabola is horizontal (the curves open left and right). If the y term is positive, the parabola is vertical (the curves open up and down). Unlike an ellipse, it does not matter which denominator is larger.
2. The center point. As with all conic sections, the center point is (h, k). Notice that the h is always with the x and the k is always with the y. There is also a negative in front of each, so you must take the opposite.
3. The a and b values. These will be needed to graph the parabola. Notice that a is always under the positive term and b is always under the negative term.
2. The center point. As with all conic sections, the center point is (h, k). Notice that the h is always with the x and the k is always with the y. There is also a negative in front of each, so you must take the opposite.
3. The a and b values. These will be needed to graph the parabola. Notice that a is always under the positive term and b is always under the negative term.
Let's identify some key information from these hyperbolas:
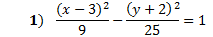
First of all, we know it is a horizontal hyperbola since the x term is positive. That means the curves open left and right.
Next, we can find the center point by identifying h and k. h is with the x, and we must take the opposite, so h = 3. k is with the y and we must take the opposite so k = -2. The center point is (3, -2).
We can find a and b by taking the square root of the denominators. The square root of 9 is 3 so a = 3. The square root of 25 is 5, so b = 5. Notice that a is not always the largest number.
Summary: This is a horizontal hyperbola. The center is at (3, -2). a = 3, b = 5
Next, we can find the center point by identifying h and k. h is with the x, and we must take the opposite, so h = 3. k is with the y and we must take the opposite so k = -2. The center point is (3, -2).
We can find a and b by taking the square root of the denominators. The square root of 9 is 3 so a = 3. The square root of 25 is 5, so b = 5. Notice that a is not always the largest number.
Summary: This is a horizontal hyperbola. The center is at (3, -2). a = 3, b = 5
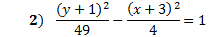
First of all, we know it is a vertical hyperbola since the y term is positive. That means the curves open up and down.
Next, we can find the center point by identifying h and k. Remember h is with the x and k is with the y. We must take the opposite of each. So our center point is (-3, -1)
We can find a and b by taking the square root of the denominators. a = 7 and b = 2 (Remember a is always with the positive term.)
Summary: This is a vertical hyperbola. The center is at (-3, -1). a = 7, b = 2
Next, we can find the center point by identifying h and k. Remember h is with the x and k is with the y. We must take the opposite of each. So our center point is (-3, -1)
We can find a and b by taking the square root of the denominators. a = 7 and b = 2 (Remember a is always with the positive term.)
Summary: This is a vertical hyperbola. The center is at (-3, -1). a = 7, b = 2
Practice: Tell whether each parabola is vertical or horizontal. Then find the center point, a, and b.
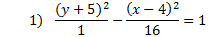
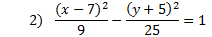
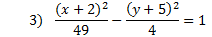
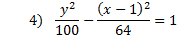
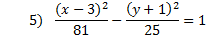
Answers: 1) vertical, center: (4, -5), a = 1, b = 4 2) horizontal, center: (7, -5), a = 3, b = 5 3) horizontal, center: (-2, -5), a = 7, b = 2 4) vertical, center: (1, 0) a = 10, b = 8 5) horizontal center: (3, -1), a = 9, b = 5
|
Related Links: Math Fractions Factors |
