Understanding Parabolas
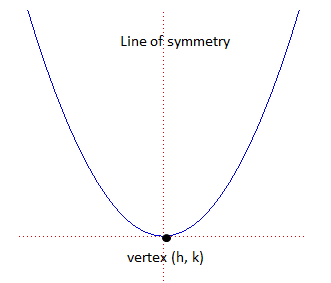
Notice that the parabola a line of symmetry, meaning the two sides mirror each other.
There are two patterns for a parabola, as it can be either vertical (opens up or down) or horizontal (opens left or right.)
Patterns:
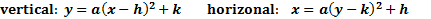
Let's look at a few key points about these patterns:
- If the x is squared, the parabola is vertical (opens up or down). If the y is squared, it is horizontal (opens left or right).
- If a is positive, the parabola opens up or to the right. If it is negative, it opens down or to the left.
- The vertex is at (h, k). You have to be very careful. Notice how the location of h and k switches based on if the parabola is vertical or horizontal. Also, the coordinate inside the parenthesis is negative, but the one outside is not.
Let's look at a couple parabolas and see what we can determine about them.
1.
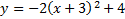
First, we know that this parabola is vertical (opens either up or down) because the x is squared. We can determine it opens down because the a (-2) is negative.
Next we can find the vertex (h, k). For a vertical parabola, h is inside parenthesis, and since there is a negative in the pattern, we must take the opposite. So h = -3. k is outside, and the sign in the pattern is positive, so we will keep this number as is. k = 4. Thus, our vertex is (-3, 4).
Summary: This is a vertical parabola that opens down. Its vertex is (-3, 4).
Next we can find the vertex (h, k). For a vertical parabola, h is inside parenthesis, and since there is a negative in the pattern, we must take the opposite. So h = -3. k is outside, and the sign in the pattern is positive, so we will keep this number as is. k = 4. Thus, our vertex is (-3, 4).
Summary: This is a vertical parabola that opens down. Its vertex is (-3, 4).
2.
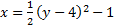
First, we know that this parabola is horizontal (opens either left or right) because the y is squared. We can determine it opens to the right because the a (1/2) is positive.
Next we can find the vertex (h, k). For a horizontal parabola, h is outside parenthesis, and since there is a positive in the pattern, we will leave it as is. So h = -1. k is inside, and the sign in the pattern is negative, so we will take the opposite. k = 4. Thus, our vertex is (-1, 4).
Summary: This is a horizontal parabola that opens to the right. Its vertex is (-1, 4).
Next we can find the vertex (h, k). For a horizontal parabola, h is outside parenthesis, and since there is a positive in the pattern, we will leave it as is. So h = -1. k is inside, and the sign in the pattern is negative, so we will take the opposite. k = 4. Thus, our vertex is (-1, 4).
Summary: This is a horizontal parabola that opens to the right. Its vertex is (-1, 4).
Practice: Determine whether the parabola opens up, down, left, or right. Then find its vertex.
1.
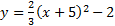
2.
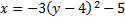
3.
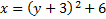
4.
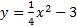
5.
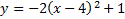
Answers: 1) Opens up, vertex: (-5, -2) 2) Opens to the left, vertex: (-5, 4) 3) Opens to the right, vertex: (6, -3) 4) Opens up, vertex: (0, -3) 5) Opens down, vertex: (4, 1)
|
Related Links: Math Fractions Factors |
