Using the Law of Cosines to Find the Third Side
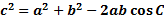
In which c is the side across from angle C.
Just like the Law of Sines, the Law of Cosines works for any triangle, not just right triangles.
In particular, the Law of Cosines can be used to find the length of the third side of a triangle when you know the length of two sides and the angle in between.
To use the Law of Sines to find a third side:
1. Identify angle C. It is the angle whose measure you know.
2. Identify a and b as the sides that are not across from angle C.
3. Substitute the values into the Law of Cosines.
4. Solve the equation for the missing side.
2. Identify a and b as the sides that are not across from angle C.
3. Substitute the values into the Law of Cosines.
4. Solve the equation for the missing side.
Examples:
1. Find the length of the third side:
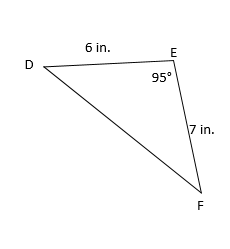
We must first determine which angle is C. We are told the measure of angle E, so that will be C in our formula. Thus the empty side will be side c and 6 and 7 will be a and b:
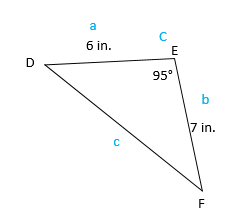
Now we will subsitute into the formula:
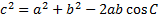
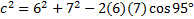
And solve the equation:
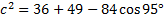
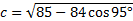
Carefully input this into our calculator:
c ≈ 9.6 in.
2. Find the length of side c if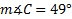
, a = 5 ft. and b = 8 ft.
Practice: Use the Law of Cosines to find the length of the third side for each triangle. Round your answer to the nearest tenth.We must first determine which angle is C. We are told the measure of angle E, so that will be C in our formula. Thus the empty side will be side c and 6 and 7 will be a and b:
Now we will subsitute into the formula:
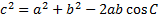
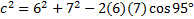
And solve the equation:
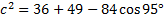
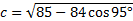
Carefully input this into our calculator:
c ≈ 9.6 in.
2. Find the length of side c if
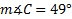, a = 5 ft. and b = 8 ft.
We could draw a picture, but since everything is clearly labeled, we don't need to. Our known angle is already called angle C and the sides are already labeled as a andb, so we are ready to subsitute:
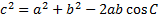
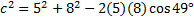
And solve the equation:
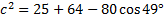
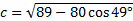
Carefully input this into our calculator:
c ≈ 6.0 ft.
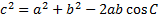
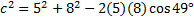
And solve the equation:
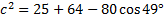
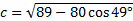
Carefully input this into our calculator:
c ≈ 6.0 ft.
Hint: Draw a picture if needed.
1. 
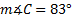, a = 10 cm. and b = 6 cm.
2.
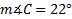, a = 2 in. and b = 9 in.
3.
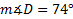, a = 4 m. and b = 2 m.
4.
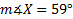, y = 8 mm. and z = 5 mm.
5.
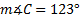, d = 9 ft. and e = 12 ft.
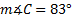, a = 10 cm. and b = 6 cm.2.
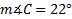, a = 2 in. and b = 9 in.3.
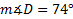, a = 4 m. and b = 2 m. 4.
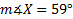, y = 8 mm. and z = 5 mm.5.
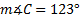, d = 9 ft. and e = 12 ft.
Answers: 1) 11.0 cm 2) 7.2 in. 3) 3.9 m. 4) 6.9 mm. 5) 18.5 ft.
|
Related Links: Math Fractions Factors |