Using the Law of Sines to Find an Unknown Angle
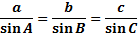
a stands for the side across from angle A, b is the side across from angle B, and c is the side across from angle C.
This law is extremely useful because it works for any triangle, not just a right triangle. In particular, it can often be used to find an unknown angle or an unknown side of a triangle.
To find an unknown angle using the Law of Sines:
1. Substitute the known values into the formula.
2. Remove the fraction that is unhelpful.
3. Solve the remaining equation.
Examples: 2. Remove the fraction that is unhelpful.
3. Solve the remaining equation.
1. Find the measure of angle B.
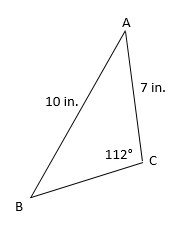
First we'll subsitute all the information we know into the Law of Sines:
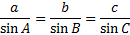
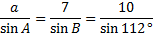
Now we'll eliminate the fraction we don't need. The 3rd fraction has both pieces of information and the second fraction contains the angle we are solving for. But the first fraction is not helpful. Let's rewrite the law without it:
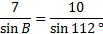
Now we'll cross multiply and solve the equation:
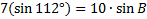
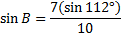
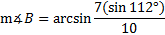
Carefully input this into your calculator. Remember on your calculator the arcsin button may look
like this:
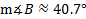
2. Find the measure of angle A.
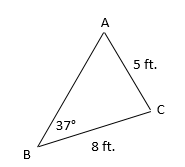
First we'll subsitute all the information we know into the Law of Sines:
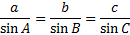
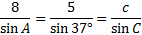
Now we'll eliminate the fraction we don't need. The 1st fraction contains the angle we are solving for and the 2nd faction contains both pieces of information. The 3rd fraction, however, is completely unhelpful. Let's rewrite the law without it"
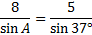
Now we'll cross multiply and solve the equation:
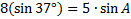
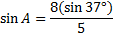
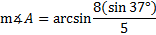
Carefully input this into your calculator.
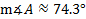
Note: We are not yet considering the ambiguous case. We will study this special situation in a future lesson.
Practice:Use the Law of Sines to find the given angle for each triangle. Round your answer to the nearest tenth if necessary.
Note: If you are not given a picture (as in these questions), you can either draw a picture or simply substitute the information right into the law.
Answers: 1) 51.2° 2) 34.4° 3) 14.5° 4) 30.1° 5) 30.0°
First we'll subsitute all the information we know into the Law of Sines:
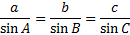
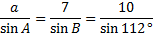
Now we'll eliminate the fraction we don't need. The 3rd fraction has both pieces of information and the second fraction contains the angle we are solving for. But the first fraction is not helpful. Let's rewrite the law without it:
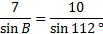
Now we'll cross multiply and solve the equation:
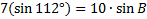
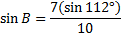
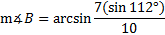
Carefully input this into your calculator. Remember on your calculator the arcsin button may look
like this:
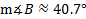
2. Find the measure of angle A.
First we'll subsitute all the information we know into the Law of Sines:
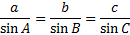
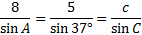
Now we'll eliminate the fraction we don't need. The 1st fraction contains the angle we are solving for and the 2nd faction contains both pieces of information. The 3rd fraction, however, is completely unhelpful. Let's rewrite the law without it"
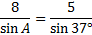
Now we'll cross multiply and solve the equation:
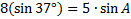
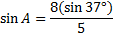
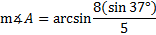
Carefully input this into your calculator.
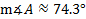
Note: We are not yet considering the ambiguous case. We will study this special situation in a future lesson.
Practice:Use the Law of Sines to find the given angle for each triangle. Round your answer to the nearest tenth if necessary.
Note: If you are not given a picture (as in these questions), you can either draw a picture or simply substitute the information right into the law.
1) Find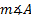 
if a = 4 in., b = 5 in., and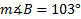 
2) Find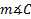
if a = 3 cm., c = 2 cm., and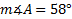 
3) Find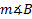
if c = 6 ft., b = 4 ft., and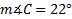 
4) Find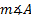 if a = 3 yd, c = 4 yd., and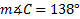 
5) Find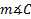 if b = 10 mm., c = 5 mm., and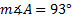 
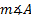if a = 4 in., b = 5 in., and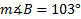 2) Find
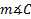if a = 3 cm., c = 2 cm., and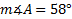 3) Find
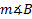if c = 6 ft., b = 4 ft., and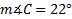 4) Find
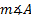if a = 3 yd, c = 4 yd., and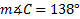 5) Find
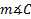if b = 10 mm., c = 5 mm., and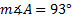
Answers: 1) 51.2° 2) 34.4° 3) 14.5° 4) 30.1° 5) 30.0°
|
Related Links: Math Fractions Factors |