Adding Integers (Positive + Negative)
Take a look at this problem on the number line:
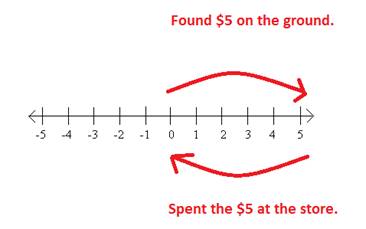
Positve 5 and negative 5 are also called opposites. When we add opposites together, we end up at zero.
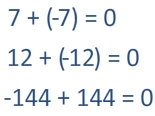
Take a look at it another way:
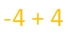
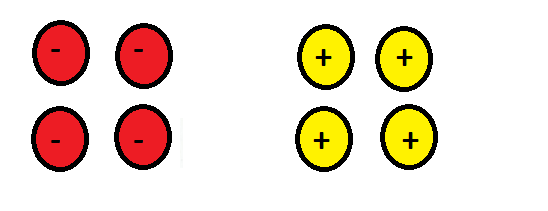
Each positive chip will cancel out with each negative and there will be no chips left. So we can see that -4 + 4 = 0.
We can use this property to help us add other integers. Here are some examples:
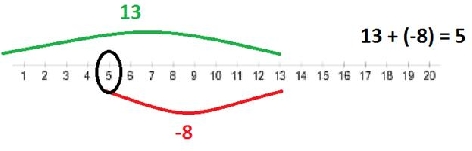
1.)13 + (-8)
Method 1 - Rewrite the problem so that we have opposites that can cancelout.
13 is also 5 + 8, so we will replace the 13 with 5 + 8

Therefore 13 + (-8) = 5.
Method 2 - The number line.
When you add a positive on the number line, you move to the right, towards the larger numbers.
When you add a negative on a number line you move to the left.
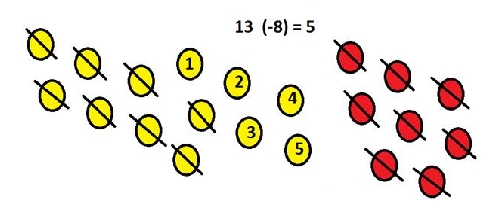
Method 3 - Using the chips. We can cross out one positive chip for every one negative chip.
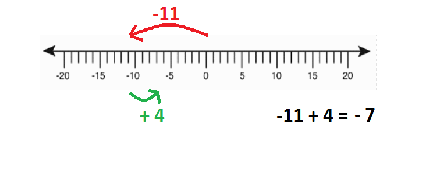
2.)-11 + 4
Therefore 13 + (-8) = 5.
Method 2 - The number line.
When you add a positive on the number line, you move to the right, towards the larger numbers.
When you add a negative on a number line you move to the left.

Method 3 - Using the chips. We can cross out one positive chip for every one negative chip.

Method 1- We can use opposites. -11 is the same as -7 + -4
-7 + -4 + 4
-7 + 0
-7
Method 2- The number line. We will start at -11 and then add positive 4. So we will need to travel to the right.
Method 3- Using the chips.
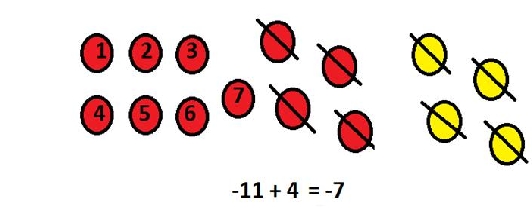
In each method, the opposites are adding to a total of zero to give us the answer. Once you get good at adding integers, you can also just think of the rule.
-7 + -4 + 4
-7 + 0
-7
Method 2- The number line. We will start at -11 and then add positive 4. So we will need to travel to the right.

Method 3- Using the chips.
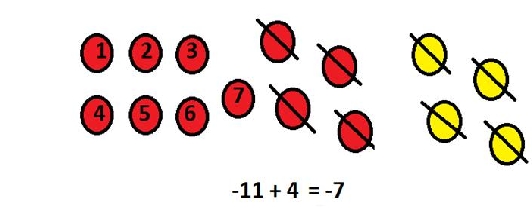
In each method, the opposites are adding to a total of zero to give us the answer. Once you get good at adding integers, you can also just think of the rule.
Rule for adding integers with different signs:
Subtract the absolute values of the numbers and the use the sign of the larger absolute value.
Example:14+(-9)
This is the same as 14 - 9 = 5. So, 14 + (-9) = 5
Example:-23+13
Think of this as 23 - 10 = 13. However, 23 is larger than 13, so we take the sign of the 23, which happens to be negative. So, -23 + 13 = -10.
Example:11+(-18)
This is the same as 11 - 18. This can also be thought of as 18 - 11 = 7, but the larger absolute value (18) has a negative sign. So the answer is -7. 11 + (-18) = -7
As you can see, no matter which method you choose, the opposites will cancel out, and you will get to the answer. As you begin adding integers with different signs, you may want to use one of the first three methods. As you get better at this, just using the rule should help you get to the answer.
Related Links:
Math
Fractions
Factors
