Adding and Subtracting Mixed Numbers
Adding and subtracting a mixed number is very similar to adding and subtracting proper fractions. The big difference is that there are whole numbers in the mix.
Check some examples:
Related Links:
Math
Fractions
Factors
Check some examples:
1.) 
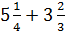
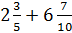
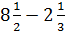
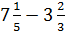
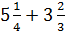
Step 1: Separate the whole number from the fractions.
(5 + 3) + (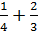
)
Step 2: Now we will add the whole numbers together and add the fractions together.
5 + 3 = 8
To add the fractions we need common denominators.
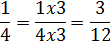
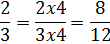
Now that we have common denominators, we can add the numerators and leave the denominator the same.
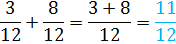
Step 3: Write the answer to both parts as a mixed number:
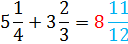
2.) (5 + 3) + (
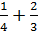)Step 2: Now we will add the whole numbers together and add the fractions together.
5 + 3 = 8
To add the fractions we need common denominators.
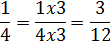
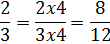
Now that we have common denominators, we can add the numerators and leave the denominator the same.
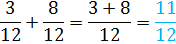
Step 3: Write the answer to both parts as a mixed number:
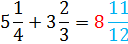
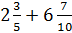
We will follow the same steps in this example with one slight change at the end.
Step 1: Separate the whole number from the fraction part of each number.
2 + 6 +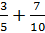
Step 2: Add the whole numbers and then add the fractions.
2 + 6 = 8
Again, we will need to get common denominators so that we can add the fractions.
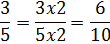
The second fraction already has 10 as the denominator, so we are ready to add.
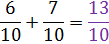
In this example, the answer to the fraction part is an improper fraction. Change it to a mixed number so that it can be added to the whole number part of the problem.
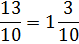
Step 3: Add the whole number answer to the fraction answer.
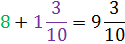
Therefore,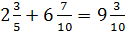
The steps for subtracting mixed numbers is very similar to the steps for adding mixed numbers. However, before you work with the whole number and fraction, you should get common denominators and make sure that you do not need to borrow. We will look at this example where you do not need to borrow and in the next example you will need to borrow so that you can see both.
3.) Step 1: Separate the whole number from the fraction part of each number.
2 + 6 +
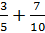
Step 2: Add the whole numbers and then add the fractions.
2 + 6 = 8
Again, we will need to get common denominators so that we can add the fractions.
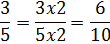
The second fraction already has 10 as the denominator, so we are ready to add.
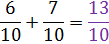
In this example, the answer to the fraction part is an improper fraction. Change it to a mixed number so that it can be added to the whole number part of the problem.
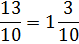
Step 3: Add the whole number answer to the fraction answer.
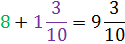
Therefore,
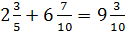
The steps for subtracting mixed numbers is very similar to the steps for adding mixed numbers. However, before you work with the whole number and fraction, you should get common denominators and make sure that you do not need to borrow. We will look at this example where you do not need to borrow and in the next example you will need to borrow so that you can see both.
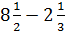
Step 1: Get common denominators.
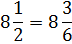
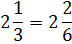
We can subtract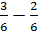
without borrowing. So we are ready to proceed.
Step 2: Subtract the whole numbers and subtract the fractions.
8 - 2 = 6
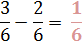
Step 3: Write the answer as a mixed number.
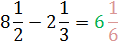
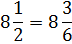
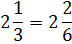
4.) We can subtract
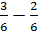without borrowing. So we are ready to proceed.Step 2: Subtract the whole numbers and subtract the fractions.
8 - 2 = 6
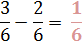
Step 3: Write the answer as a mixed number.
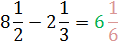
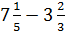
Step 1: Get common denominators and determine if you need to borrow.
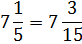
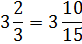
In this example, we have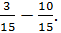
This is an example where we need to borrow 1 from 7. However, keep in mind that 1 is really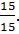 
So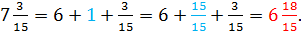
Step 2: Subtract the whole numbers and the fractions.
The new problem is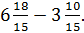
6 - 3 = 3
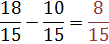
Step 3: Write the answer as a mixed number.
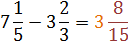
There are other methods, like using improper fractions, but if you need the answer to be a mixed number, this can become difficult. The numbers can get very large and that makes it easier to make mistakes.
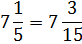
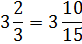
In this example, we have
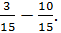This is an example where we need to borrow 1 from 7. However, keep in mind that 1 is really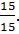 So
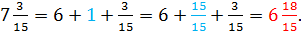
Step 2: Subtract the whole numbers and the fractions.
The new problem is
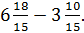
6 - 3 = 3
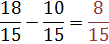
Step 3: Write the answer as a mixed number.
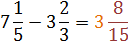
There are other methods, like using improper fractions, but if you need the answer to be a mixed number, this can become difficult. The numbers can get very large and that makes it easier to make mistakes.
Related Links:
Math
Fractions
Factors