A multiple is the number you get from multiplying a given number by a whole number.

(Remember that the whole numbers are 0, 1, 2, 3, 4, 5,....)

For example, the multiples of 5 would be 0, 5, 10, 15, 20, 25, 30, 35, 40,....

Multiples can go on forever and ever. Multiples might also look like "skip counting".

We can also think of the multiples as the answers to a series of multiplication questions. So the multiples of 5 would be the answers to 5 x 0, 5 x 1, 5 x 2, 5 x 3, 5 x 4, 5 x 5, ....)

Sometimes we need to find the LCM, or Least Common Multiple of two or more numbers. This is the smallest multiple that two numbers have in common.

There are several methods for calculating the LCM.



Method 1:Lists

In this method, you simply list out several multiples of each number and then look for the smallest one that both numbers have in common.

Example: What is the LCM of 36 and 20?

36: 36, 72, 108, 144, 180, 216,....

20: 20, 40, 60, 80, 100, 120, 140, 160, 180, 200,....

180 is the smallest multiple that both numbers have in common. So 180 is the LCM of 36 and 20.


Method 2: Upside Down Division

Using the same steps that are used for calculating the GCF of two numbers can also give us the LCM in the upside down division.

Example: What is the LCM of 45 and 80?

We will place the two numbers in the upside down division to start.



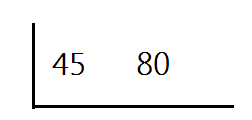
Then we will divide both numbers by the same amount.



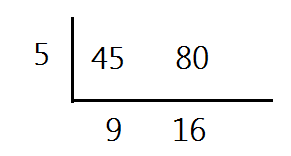
When the two numbers do not have any more common factors, we call them relatively prime and then we are ready to find the LCM. So the next step is to multiply all the numbers around the outside of the division bar. The numbers should be in the shape of a "bubble L".



So the LCM of 45 and 80 is 5 x 9 x 16 = 720.

This method is great because you don't have to make really long lists in order to find the LCM.


Method 3: Using Prime Factorization

Yet another method would be to list out the prime factorization of each number and then multiply all the terms that the two do not have in common.

Example: What is the LCM of 120 and 27?

The prime factorization of 27 = 3 x 3 x 3

The prime factorization of 120 = 2 x 2 x 2 x 3 x 5

Now we will line up the prime factorizations.



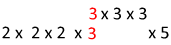
We will only use the 3s that the numbers have in common once.



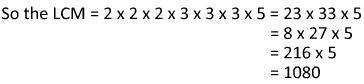
Here we can see that the LCM of 27 and 120 is 1080.

How can I use this?

You may wonder why LCM is important. One example would be what is called "next time" problems.

Example: Every 12th day Emily volunteers at the nursing home. Every 15th day David volunteers at the nursing home. Emily and David were both volunteering today. How many days will pass before David and Emily will be volunteering together again?

This question is asking for the LCM.



If we look diagonally at the upside down division,we get even more inforamtion.David will have volunteered 4 times and Emily will have volunteered 5 times in between.

Example: Hot dogs come in packages of 6 and hot dog buns come in packages of 8. What is the least number of packages of each would we need to buy to have an equal amount of both?

This is also an LCM question.



This means that we would need to buy 24 hot dogs and 25 buns.This doesn't quite answer the question yet.Again,we can use the diagonals.Across from the account of hot dogs,we can see that we would need 4 packages.(4 x 6 = 24).Across from the buns,we can see that we need 3 packages. (3 x 8 = 24)

Let's Review: The multiples of numbers are made by multiplying the number by whole numbers. So multiples of 11 would be 0, 11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121,....The least common multiple of two or more numbers is the smallest multiple that both/all numbers have in common. You can find the LCM by making lists, using upside down division or prime factorization. LCMs are important because they help us problem solve.