You may already be familiar with the correct order for solving the four operations; multiplying & dividing, then adding & subtracting.

However, there are several other steps that can be added to a math problem. What order should we follow now? There are several acronyms to help you remember the correct order of operations. One of the most popular would be PEMDAS or "Please Excuse My Dear Aunt Sally." No matter how you remember the letters of PEMDAS, you still have to know how to use the letters to help you solve.

Let's start with a review of what each letter stands for.

P = Parentheses (you can include brackets here as well)

( ), [ ], { }

E = Exponents example 2³, where the 3 is the exponent

M or D = Multiplication or Division

A or S = Addition or Subtraction

You can follow these somewhat in order. Let's explain what that means. Notice how the M and D are paired. The A and S are also paired. When you get to the M and D in the steps, you need to look for both operations at the same time and do whichever is on the left first. The same thing goes with A and S. You will need to work these problems from left to right as well. If subtraction is on the left, before addition, you will complete it before the addition.

Let's put this all to work. Here are some examples.

1.) 15 x 4 - (6 - 3) x 2³

Step 1: You can underline or highlight the first step to help you keep your work organized.

15 x 4 - (6 - 3) x 2³ Look for parentheses first.

15 x 4 - 3 x 2³ The next step is to simplify anything with an exponent.

15 x 4 - 3 x 8 The third steps is to complete the
multiplication and division going from left to right.

60 - 3 x 8. Then we end with the addition and subtraction,
also working from left to right.

60 - 24

36

2.) 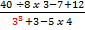This example does not include any parentheses.
 So the first step is to start with the exponents.

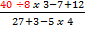Now, because the problem is a large complicated fraction,
we will start by simplifying on the top, using the order of
operations. Remember that when looking for the division and multiplication, you need to work from left to right.







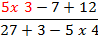
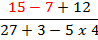
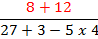
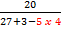Now that the top is simplified, we can use the order of
operations to simplify the bottom. Start with all the
multiplying and dividing and then move to the
adding and subtracting.





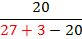
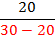
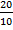Now that both the top and bottom are simplified, the last step
 is to divided the two numbers, 20 ÷ 10 = 2

2

3.) |4² - 30| + 5⁰ x 13 This example includes the absolute value bars. You can think   of these like parentheses. So we will start our solving inside
  the bars.

|4² - 30| + 5⁰ x 13

|16 - 30| + 5⁰ x 13

|-14| + 5⁰ x 13

14 + 5⁰ x 13 Next, we move on to simplify the terms with exponents.

14 + 1 x 13 The third step is to look for multiplication and division.

14 + 13 Then we end with the addition and subtraction.

27


Related Links:
Order of Operations
Math
Fractions
Factors