Sometimes data sets have data values that are all very close to each other except for one or two that are really, really large or really, really small.

Let's see what happens to the measures of center when an outlier is added.

First, we will take a look at a typical set of data. This set shows the heights of a group of kids.

42 in, 38 in, 40 in, 38 in, 39 in, 44 in, 41 in, 40 in

We will determine the mean, median and mode of the set of heights.

Mean =

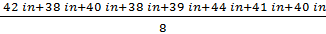
Mean =

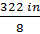
Mean = 40.25 in



Median = 40 in

Mode: 38 in and 40 in (both appear twice in the data)

Now that we have the mean, median and mode of the typical data, let's add a very tall person to the group of students.



Mean =

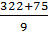
Mean =

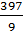
Mean = 44.11 in



Median = 40 in

Mode: 38 in and 40 in

Here we can see that an outlier that is larger than all of the other data values increases the mean, but it did not affect the median or mode in this example.

When there is an outlier included in the data, the mean is typically not going to represent the data as well as the median.

Check out what could happen to your average in math when you add a zero in for your grade.

Let's say that you had the following grades: 87, 92, 90, 88, 85, 81, 94. Calculate the mean, median and mode of the data.

Mean =

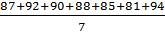
Mean =

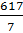
Mean = 88.1428



Median = 88

Mode: No Mode (none of the numbers repeat)

Now, let's say that you forget to turn in the next assignment. So now your scores read:

Mean =

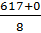
Mean =

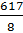
Mean = 77.125



Median = 87.5

Mode: No mode (still no numbers repeating)

Notice here that adding a very small number that is outside the typical values lowers the mean. The median and mode stay close to the same

Would we say that this student typically scores about a 77% on tasks? That doesn't fit the data and doesn't describe the student very well.

An outlier can really change the mean and make it not as good of a description as the median and possibly the mode.





Related Links:
Math
Fractions
Factors