Each of the trigonometric functions sine, cosine, tangent, secant, cosecant and cotangent has an inverse (with a restricted domain). The inverse is used to obtain the measure of an angle using the ratios from basic right triangle trigonometry. The inverse of cosine is denoted as Arccosine or on a calculator it will appear as acos or cos^-1. Note: this does NOT mean cosine raised to the negative one power.

Let's look at an example of how to use the inverse cosine function to find the measure of an angle in a right triangle. (triangle not drawn to scale)



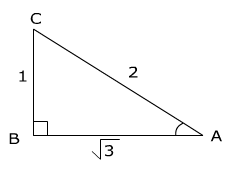
To find the measure in degrees of angle A using the cosine inverse, recall that



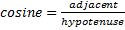
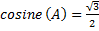
Use a scientific calculator 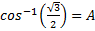     *Make sure your calculator is in degree mode

30° = A

Let's look at an application problem.

Suppose a building is 40 feet tall and a fireman's ladder is 60 feet long. What is the measure of the angle that is formed by the building and the ladder?

Begin by creating a diagram of the given information.



Recall that      cosine θ =

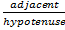
Therefore        cosine θ =

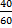
Use the inverse of cosine 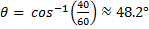     rounded to the nearest tenth

If it is understood how to use the basic right triangle trigonometric ratios, then the inverse can be used to find a missing angle measure in any right triangle. If all three sides of the triangle are given then any of the trig ratios can be used and an equivalent angle measure will be derived. Sine, cosine, secant, tangent, cosecant and cotangent are all functions however, the inverses are only a function when given a restricted domain.

Related Links: Math Trigonometry Inverse Sine Function (Arcsine) Inverse Tangent Function (Arctangent)