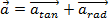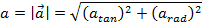Rotational Kinematic Formulas
The motion of a rotating object can be described using angular displacement, angular velocity, and angular acceleration. Angular displacement is a measure of the change in the angular coordinate θ. Angular velocity is the rate of change of the angular coordinate with respect to time. Angular acceleration is the rate of change of angular velocity with respect to time.
The angular coordinate and angular displacement are measured in radians, which is a "stand-in", or placeholder unit. The angular coordinate is actually a ratio of lengths, and is therefore dimensionless. It is important to remember that radians are a convenient way to express the dimensionless coordinate when discussing rotational motion.
The SI unit of angular velocity is radians per second, which can be written in a number of ways. Writing the units of angular velocity as
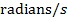
,
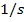
, or as
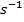
are all equivalent. The SI unit of angular acceleration is radians per second squared, which can be written in a number of ways. Writing the units of angular acceleration as
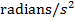
,
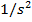
, or as
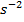
are all equivalent.
In a previous section, formulas for one-dimensional kinematics that related linear displacement, velocity, and acceleration to each other were derived. In this section, similar formulas for rotational kinematics will be developed. In AP Physics, changes in angular acceleration are typically not considered, and so these rotational kinematic formulas assume constant angular acceleration.
Previously, formulas were introduced for average angular velocity and constant angular acceleration,
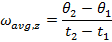
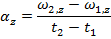
The subscript "z" in these formulas indicate that the motion described is a rotation around the z axis. This is true when the rotation takes place in the xy plane. The axis of rotation is always perpendicular to the plane of the motion. The angular velocity and angular acceleration are both vectors, and so when we choose to define the rotation with the z axis as the axis of rotation, the full vectors and their components are,
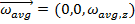
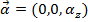
If the starting time is set to zero, t
1 = 0, then the angular displacement and angular velocity at t
1 = 0 are the "initial conditions". The initial conditions can be assigned distinct labels. The initial angular displacement has the value θ
1 = θ
0, and the initial angular velocity has the value
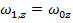
. At a later time t
2 = t, the angular displacement is θ
2 = θ, and the angular velocity is
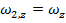
.
For a rotation around the z axis, the formulas for the average angular velocity and constant angular acceleration are,
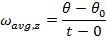
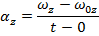
These formulas can be used to derive other formulas that relate the angular displacement, angular velocity, and angular acceleration.
Angular Velocity
A formula to calculate the angular velocity of an object rotating around the z axis at time t can be made by rearranging the above formula for constant angular acceleration,
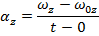
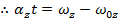
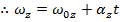
This formula makes it possible to calculate how the angular velocity changes as a result of an angular acceleration.
Angular Displacement
A formula to calculate a new angular displacement of an object rotating around the z axis at time t can be made using the formula for average angular velocity,
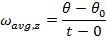
As long as the angular acceleration is constant, we can develop another formula for the average angular velocity. In general, the way to calculate the average of a group of numbers is to add them together, and divide by how many numbers are being averaged. If
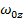
is the start value, and
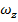
is a later value of the angular velocity, the average of these is equal to,
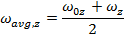
The formula for
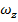
shown previously in this section can be substituted in to this formula,
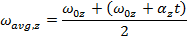
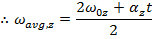
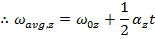
This formula can be set equal to the other formula for
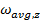
,
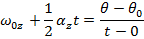
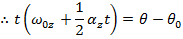
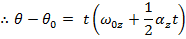
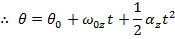
This formula can be used to calculate the angular displacement that results when there is an initial angular velocity
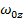
, and a constant angular acceleration
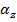
. This formula can also be used in situations with no initial angular velocity by setting
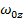
equal to zero, or in situations with no angular acceleration by setting
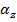
equal to zero.
Angular Velocity, Angular Acceleration, and Angular Displacement
A formula to calculate the angular velocity in a different way, using the initial angular velocity, angular acceleration, and the angular displacement, can be made using the formulas developed in this section,
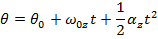
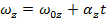
The formula for angular velocity can be rearranged to isolate for the time t,
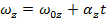
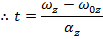
This formula for time can be substituted in to the formula for angular displacement,
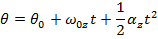
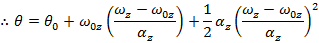
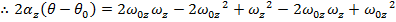
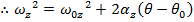
This formula is useful because it completely excludes the time variable t. It relates the initial and final angular velocities, the angular acceleration, and the change in the angular displacement. For this reason it is very useful for problems in which the amount of time between the initial and final states is unknown.
Angular Displacement and Angular Velocity
A formula to calculate the angular displacement using the angular velocity can be made using formulas for the average angular velocity,
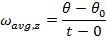
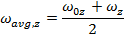
Setting these formulas equal to each other,
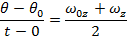
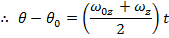
This formula is useful because it excludes the angular acceleration, and relies on the initial and final angular velocities to determine the change in angular displacement. It is useful for problems in which the initial and final velocities are known, but the angular acceleration is unknown.
Rotational Kinematics Summary
The four formulas for rotational kinematics are,
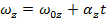
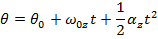
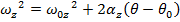
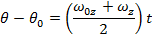
These can be used to solve a wide range of rotational motion problems.
Relating Linear and Angular Kinematics
The formulas for rotational/angular kinematics discussed in this section treat the motion of objects only in terms of angles. Imagine a circular object, like a disc, with a rotational axis perpendicular to the surface. Imagine a line that extends from the central axis to the outside of the disc. All along that line, all of the points on the disc have the same angular displacement. Every point has the same angular velocity and angular acceleration. If we now want to know the velocity or acceleration of a specific point is, we need to convert from angular to linear kinematics.
First, we have to choose a specific point within the rotating object. If we choose a point that has angular displacement θ and is a distance r from the center axis, as the object rotates, the object moves a distance s around the axis. This circular path s is called an arc. An arc of length s around the outside edge of a circle of radius r can be related to the angular coordinate using the formula,
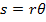
Both s and r have units of length, so in SI units, they are measured in meters. The angular displacement is measured in the "stand-in" unit radians.
A vector pointing from the axis to the point P is called the radial vector,
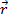
. Its magnitude is the radius r. The linear velocity vector
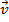
of the point P is always perpendicular to this radial vector
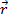
. The magnitude of the linear velocity can be found by multiplying the magnitude of the angular velocity by the radius,
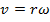
The SI unit for linear velocity is
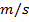
, the unit for radius is m, and the unit for angular velocity can be written as
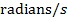
, or simply
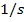
.
The acceleration of a rotating point P on the object has two components. The first component is related to the angular acceleration of the point, and is always perpendicular to the radial vector
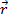
. This component can be labeled the
tangential component of acceleration, because it is always tangent to the circular path of the rotation. The symbol for the tangential acceleration vector is
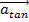
. The magnitude of the tangential acceleration can be found by multiplying the magnitude of the angular acceleration by the radius,
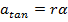
The SI unit for tangential acceleration is
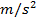
, the unit for radius is m, and the unit for angular acceleration can be written as
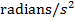
, or simply
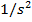
.
The second component of the acceleration of a rotating point P is the centripetal acceleration. This can also be called the
radial acceleration, because it points inward in the same direction as the radial vector. The symbol for the radial acceleration vector is
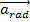
. The magnitude of the radial/centripetal acceleration was presented in a previous section as,
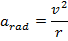
The above formula for v can be used to create a formula for the radial acceleration in terms of the angular velocity,
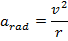
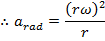
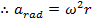
The SI unit for radial/centripetal acceleration is
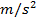
, the unit for radius is m, and the unit for angular velocity can be written as
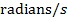
, or simply
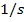
.
The total acceleration vector of the point P on a rotating object can be found using vector addition,
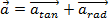
The magnitude of the total acceleration is therefore,
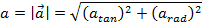
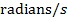 ,
, 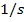 , or as
, or as 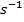 are all equivalent. The SI unit of angular acceleration is radians per second squared, which can be written in a number of ways. Writing the units of angular acceleration as
are all equivalent. The SI unit of angular acceleration is radians per second squared, which can be written in a number of ways. Writing the units of angular acceleration as 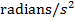 ,
, 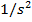 , or as
, or as 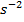 are all equivalent.
are all equivalent.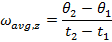
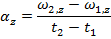
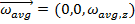
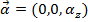
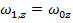 . At a later time t2 = t, the angular displacement is θ2 = θ, and the angular velocity is
. At a later time t2 = t, the angular displacement is θ2 = θ, and the angular velocity is 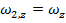 .
.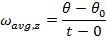
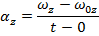
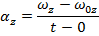
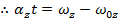
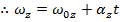
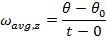
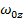 is the start value, and
is the start value, and 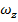 is a later value of the angular velocity, the average of these is equal to,
is a later value of the angular velocity, the average of these is equal to,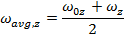
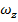 shown previously in this section can be substituted in to this formula,
shown previously in this section can be substituted in to this formula,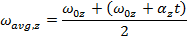
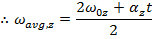
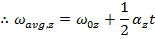
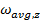 ,
,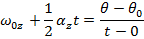
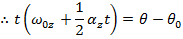
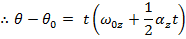
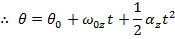
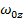 , and a constant angular acceleration
, and a constant angular acceleration 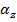 . This formula can also be used in situations with no initial angular velocity by setting
. This formula can also be used in situations with no initial angular velocity by setting 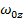 equal to zero, or in situations with no angular acceleration by setting
equal to zero, or in situations with no angular acceleration by setting 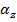 equal to zero.
equal to zero.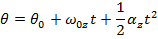
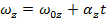
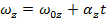
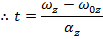
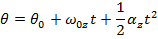
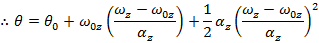
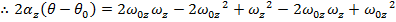
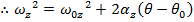
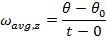
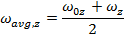
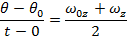
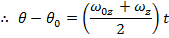
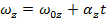
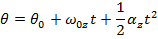
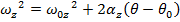
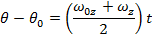
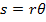
 . Its magnitude is the radius r. The linear velocity vector
. Its magnitude is the radius r. The linear velocity vector 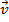 of the point P is always perpendicular to this radial vector
of the point P is always perpendicular to this radial vector 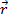 . The magnitude of the linear velocity can be found by multiplying the magnitude of the angular velocity by the radius,
. The magnitude of the linear velocity can be found by multiplying the magnitude of the angular velocity by the radius,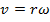
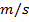 , the unit for radius is m, and the unit for angular velocity can be written as
, the unit for radius is m, and the unit for angular velocity can be written as 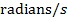 , or simply
, or simply 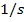 .
.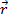 . This component can be labeled the tangential component of acceleration, because it is always tangent to the circular path of the rotation. The symbol for the tangential acceleration vector is
. This component can be labeled the tangential component of acceleration, because it is always tangent to the circular path of the rotation. The symbol for the tangential acceleration vector is 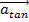 . The magnitude of the tangential acceleration can be found by multiplying the magnitude of the angular acceleration by the radius,
. The magnitude of the tangential acceleration can be found by multiplying the magnitude of the angular acceleration by the radius,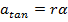
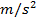 , the unit for radius is m, and the unit for angular acceleration can be written as
, the unit for radius is m, and the unit for angular acceleration can be written as 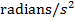 , or simply
, or simply 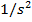 .
.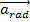 . The magnitude of the radial/centripetal acceleration was presented in a previous section as,
. The magnitude of the radial/centripetal acceleration was presented in a previous section as,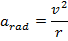
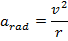
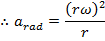
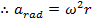
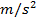 , the unit for radius is m, and the unit for angular velocity can be written as
, the unit for radius is m, and the unit for angular velocity can be written as 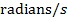 , or simply
, or simply 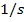 .
.