Kinematic Formulas and Freefall
Kinematic Formulas
Motion along a straight line can be described using displacement, velocity, and acceleration. Velocity is the rate of change of displacement with respect to time. Acceleration is the rate of change of velocity with respect to time. The SI unit of displacement is the meter (m), the SI unit of velocity is meters per second (m/s), and the SI unit of acceleration is meters per second squared (m/s2). There are a number of formulas that can relate these quantities to each other, which can be used in a wide variety of one-dimensional motion problems. In AP Physics, changes in acceleration are not considered, and so these kinematic formulas assume a constant acceleration.
The previous section introduced formulas for average velocity and acceleration,
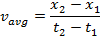
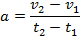
To make it clear that we are dealing with movement in one dimension, we can add the subscript "x" to the acceleration: ax. If the starting time is set to zero, t1 = 0, then the displacement and velocity at time zero are the "initial conditions". The magnitudes of the displacement and velocity have the values x1 = x0, and v1 = v0x. At some later time t2 = t, the displacement and velocity have the values x2 = x, and v2 = vx.
For movement along the x axis, the formulas for the magnitudes of the average velocity and constant acceleration are,
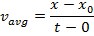
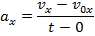
These formulas can now be used to derive other formulas that relate the displacement, velocity, and acceleration.
Velocity
A formula to calculate the magnitude of the velocity of an object at time t can be made by rearranging the above formula for constant acceleration,
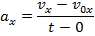
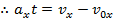
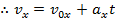
This formula makes it possible to calculate how velocity changes as a result of an acceleration.
Displacement
A formula to calculate a new displacement of an object at time t can be made using the formula for average velocity,
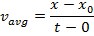
As long as acceleration is constant, we can develop another formula for the average acceleration. In general, the way to calculate the average of a group of numbers is to add them together, and divide by how many numbers are being averaged. If v0x is the start value, and vx is a later value, the average of these is equal to,
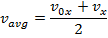
The formula for vx above can be substituted in to this formula for vavg,
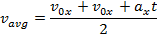
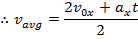
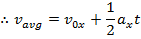
This formula can be set equal to the other formula for vavg,
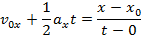
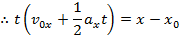
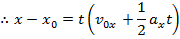
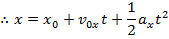
This formula can be used to calculate the magnitude of the displacement that results when there is an initial velocity v0x, and a constant acceleration ax. This formula can also be used in situations with no initial velocity by setting v0x equal to zero, or in situations with noacceleration by setting ax equal to zero.
Velocity, Acceleration, and Displacement
A formula to calculate the magnitude of velocity in a different way, using the initial velocity, acceleration, and the displacement, can be made using the first two formulas developed in this section,
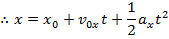
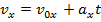
The formula for velocity can be rearranged to isolate for time t,
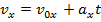
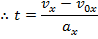
This formula for time can be substituted in to the formula for displacement,
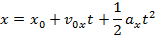
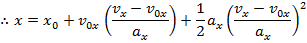
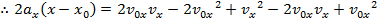
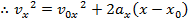
This formula is useful because it completely excludes t, the time variable. It relates the initial and final velocities, the acceleration, and the change in position. For this reason it is very useful for problems in which the amount of time is unknown.
Displacement and Velocity
A formula to calculate the displacement magnitude using velocity can be made using the formulas for the magnitude of the average velocity,
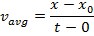
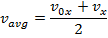
Setting these formulas equal to each other,
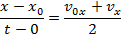
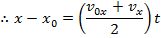
This formula is useful because it excludes the acceleration variable, and relies on the change in velocity to determine the change in position. It is useful for problems in which it is known that velocity changes, but the magnitude of the acceleration is unknown.
Summary
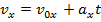
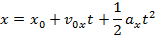
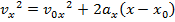
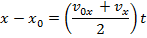
Freefall
The Earth's gravitational field causes objects to accelerate toward it. If there were no air resistance, objects of any mass dropped from the same height would fall with the same acceleration. A hammer and a feather dropped by the same person would hit the ground at the same time. Objects that are experiencing this acceleration due to gravity are said to be in "freefall". The acceleration due to gravity of an object in freefall is always directed downward, though an object that has an initial upward velocity may still be moving upward.
The symbol used for the acceleration due to gravity is g. Far from the Earth's surface, for example in orbit, the magnitude of the gravitational acceleration is different than on the surface. It also varies slightly depending on the height above sea level. However, near the Earth's surface, the magnitude of the acceleration due to gravity can be treated as a constant, equal to g = 9.80 m/s2. The acceleration due to gravity is also different on other moons or planets. Some examples are listed below.
Acceleration due to gravity near the surface of:
Motion along a straight line can be described using displacement, velocity, and acceleration. Velocity is the rate of change of displacement with respect to time. Acceleration is the rate of change of velocity with respect to time. The SI unit of displacement is the meter (m), the SI unit of velocity is meters per second (m/s), and the SI unit of acceleration is meters per second squared (m/s2). There are a number of formulas that can relate these quantities to each other, which can be used in a wide variety of one-dimensional motion problems. In AP Physics, changes in acceleration are not considered, and so these kinematic formulas assume a constant acceleration.
The previous section introduced formulas for average velocity and acceleration,
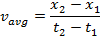
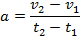
To make it clear that we are dealing with movement in one dimension, we can add the subscript "x" to the acceleration: ax. If the starting time is set to zero, t1 = 0, then the displacement and velocity at time zero are the "initial conditions". The magnitudes of the displacement and velocity have the values x1 = x0, and v1 = v0x. At some later time t2 = t, the displacement and velocity have the values x2 = x, and v2 = vx.
For movement along the x axis, the formulas for the magnitudes of the average velocity and constant acceleration are,
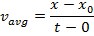
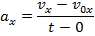
These formulas can now be used to derive other formulas that relate the displacement, velocity, and acceleration.
Velocity
A formula to calculate the magnitude of the velocity of an object at time t can be made by rearranging the above formula for constant acceleration,
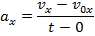
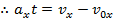
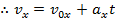
This formula makes it possible to calculate how velocity changes as a result of an acceleration.
Displacement
A formula to calculate a new displacement of an object at time t can be made using the formula for average velocity,
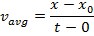
As long as acceleration is constant, we can develop another formula for the average acceleration. In general, the way to calculate the average of a group of numbers is to add them together, and divide by how many numbers are being averaged. If v0x is the start value, and vx is a later value, the average of these is equal to,
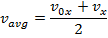
The formula for vx above can be substituted in to this formula for vavg,
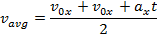
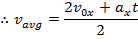
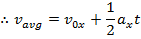
This formula can be set equal to the other formula for vavg,
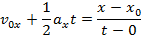
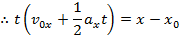
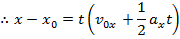
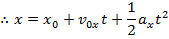
This formula can be used to calculate the magnitude of the displacement that results when there is an initial velocity v0x, and a constant acceleration ax. This formula can also be used in situations with no initial velocity by setting v0x equal to zero, or in situations with noacceleration by setting ax equal to zero.
Velocity, Acceleration, and Displacement
A formula to calculate the magnitude of velocity in a different way, using the initial velocity, acceleration, and the displacement, can be made using the first two formulas developed in this section,
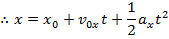
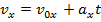
The formula for velocity can be rearranged to isolate for time t,
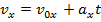
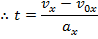
This formula for time can be substituted in to the formula for displacement,
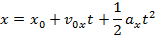
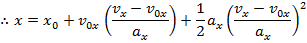
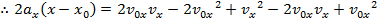
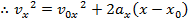
This formula is useful because it completely excludes t, the time variable. It relates the initial and final velocities, the acceleration, and the change in position. For this reason it is very useful for problems in which the amount of time is unknown.
Displacement and Velocity
A formula to calculate the displacement magnitude using velocity can be made using the formulas for the magnitude of the average velocity,
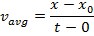
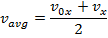
Setting these formulas equal to each other,
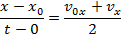
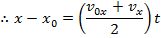
This formula is useful because it excludes the acceleration variable, and relies on the change in velocity to determine the change in position. It is useful for problems in which it is known that velocity changes, but the magnitude of the acceleration is unknown.
Summary
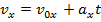
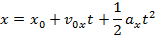
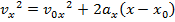
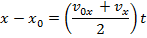
Freefall
The Earth's gravitational field causes objects to accelerate toward it. If there were no air resistance, objects of any mass dropped from the same height would fall with the same acceleration. A hammer and a feather dropped by the same person would hit the ground at the same time. Objects that are experiencing this acceleration due to gravity are said to be in "freefall". The acceleration due to gravity of an object in freefall is always directed downward, though an object that has an initial upward velocity may still be moving upward.
The symbol used for the acceleration due to gravity is g. Far from the Earth's surface, for example in orbit, the magnitude of the gravitational acceleration is different than on the surface. It also varies slightly depending on the height above sea level. However, near the Earth's surface, the magnitude of the acceleration due to gravity can be treated as a constant, equal to g = 9.80 m/s2. The acceleration due to gravity is also different on other moons or planets. Some examples are listed below.
Acceleration due to gravity near the surface of:
- Earth, 9.80 m/s2
- Earth's moon, 1.63 m/s2
- Mars, 3.72 m/s2
- Venus, 8.83 m/s2
- The sun, 274 m/s2
|
Related Links: Physics Quizzes AP Physics Notes Current, Resistance, Voltage, and Power |
