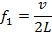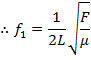Mechanical Waves
When a material or a region of space is in equilibrium, there is no motion or change in energy. A wave is a moving disturbance of that equilibrium. Waves propagate, or move from one region to another. As they do so, waves carry energy in their motion.
A wave that travels through a substance or material is called a
mechanical wave. The material it travels through is called the
medium. As the wave travels, the particles in the medium are displaced from their equilibrium positions. Examples of mechanical waves are movements or vibrations of a string, or waves moving on the surface of a body of water.
Non-mechanical waves do not travel in a medium. Visible light, and electromagnetic waves like radio are examples of non-mechanical waves.
The speed at which a wave propagates is called the wave speed. Wave speed is represented with the letter v, and the SI unit is
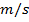
. The wave speed depends entirely on the choice of medium. For a given medium, the wave speed will always be the same.
It is important to note that the wave speed is not the same as the speed at which individual particles move. There are different types of mechanical waves, depending on the way in which the particles in the medium move. The types are:
1. Transverse waves
A transverse wave is one in which the direction of the motion of the particles is perpendicular (transverse) to the direction of travel. An example is a wave made by moving one end of a string up and down.
2. Longitudinal waves
A longitudinal wave is created when the direction of the motion of the particles is parallel to the direction that the wave travels. An example is a piston moving in a tube of water. The piston creates pressure and density changes that travel along the tube. A region of increased density is a compression. A region of reduced density is called a rarefaction.
3. Combined waves
It is also possible to create a wave with longitudinal and transverse components. An example is the motion of a flat board in a trough. Moving the board causes longitudinal motion of the water particles, but also upward motion at the surface.
A single wave is called a
wave pulse. After a wave pulse passes through a region, the medium returns to its equilibrium state. If the motion of the medium is repetitive, or periodic, then the result is a periodic wave. Each particle in the medium undergoes periodic motion as the wave propagates.
One form of periodic motion is Simple Harmonic Motion (SHM) of the medium. In this case, each particle moves according to the formula for simple harmonic motion. The formula and properties of simple harmonic motion were described in a previous section. Waves moving in simple harmonic motion are also called sinusoidal waves. A sinusoidal wave will have amplitude A, in units of meters (m), as well as a frequency f, which has units of Hertz (Hz). The period T is equal to 1/f, and has units of seconds (s). The angular frequency of a wave (or anything else) in simple harmonic motion is,
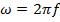
The angular frequency can also be expressed in terms of the period,
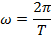
The unit of angular frequency is
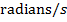
.
The shape of a sinusoidal wave is a repeating pattern. For transverse sinusoidal waves, this pattern is a series of crests and troughs. Crests are positions where the wave is displaced from equilibrium by the amplitude
A. The distance from one crest to the next, or from one trough to the next, is called the
wavelength. Wavelength has units of length, and so its SI unit is meters, m. The wavelength can be related to the wave speed and frequency with the formula,
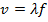
As already stated, the wave speed depends only on the medium in which the wave is moving. For that reason, if the medium does not change, an increase in the frequency means the wavelength must decrease, and a decrease in the frequency means the wavelength must increase. The product of these numbers remains the same for a given medium.
Wave Function
The mathematical description of a wave is called the
wave function. The wave function defines the position of individual particles in the medium, using x (horizontal) and y (vertical) position coordinates, as well as t to represent how the positions change with time. The positions x and y have units of length (meters), and time has units of seconds.
For a sinusoidal wave traveling in the +x direction, with increasing x defined as left to right across the page, at x = 0 the formula is,
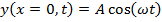
This is the formula for simple harmonic motion of a single position in the wave. The wave function must describe what happens at all x positions, though. The wave is moving at the wave speed, and so the full wave function must include that. The wave function for a sinusoidal wave (moving in the +x direction) is the formula,
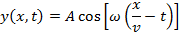
The wave function can also be written in terms of the frequency,
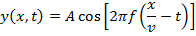
Using the formula relating period and frequency
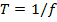
, and the formula relating the wave speed and wavelength
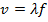
, the wave function can also be written,
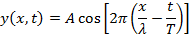
A value called the
wave number can be defined using the letter k,
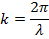
The angular frequency can be written in terms of the wave number with the formula,
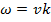
Using this formula and the wave number k, the formula for a sinusoidal wave can be written,
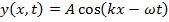 Transverse Wave Speed
Transverse Wave Speed
The most common example of a transverse wave is the result of the up-and-down movement of a string or rope. Imagine a string is perfectly flexible (free to move), and it is held with some amount of tension F to keep it straight, above the ground, in its equilibrium position. Each part of the string has a certain mass. The
linear mass density of the string is the mass per unit length. It is represented with the Greek letter
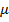
("mu"), and has units of
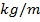
. It can be shown that the wave speed depends only on the tension in the string, and the linear mass density,
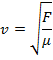
This wave speed does not depend on the amplitude or frequency of the wave. It depends only on properties related to the string, which is the medium of the wave.
Power of Wave Motion
Wave motion has energy associated with it. Power is equal to energy per unit time, and has units of Watts (W). The average power of a sinusoidal wave on a string is related to the tension F, the linear mass density
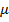
, the angular velocity
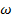
, and the amplitude of the wave A. The formula for average power
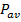
for a sinusoidal wave on a string is,
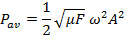 Intensity of Wave Motion
Intensity of Wave Motion
Many forms of waves, for example sound waves or seismic waves within the Earth, carry energy in all directions. Waves that travel in three dimensions have an intensity that changes with distance from the source. Intensity is the average rate at which energy is transported by the wave, per unit area. This area is a surface, perpendicular to the direction of wave propagation. Another way to say this is that intensity is the average power per unit area. Intensity is represented with the letter I, and the unit of intensity is Watts per square meter
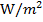
. If a wave spreads out in all directions from a source, the intensity at a certain distance is inversely proportional to the square of the distance. This means that at a distance r, the intensity is related to
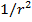
. If the power of the wave is P, then the intensity at distance r is,
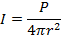
The intensity at two different distances can be compared, as long as no energy is absorbed in between. If the energy is conserved, then the power P remains the same. If the intensity is I
1 at distance r
1, and the intensity is I
2 at distance r
2, then these are related by the formula,
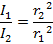
This is known as the
inverse square law for intensity.
Wave Interference and Superposition
When a wave pulse hits the boundary of the medium it moves in, all or part of the wave is
reflected. This reflected wave can overlap other wave pulses, producing
interference. Interference is the result of two or more waves passing through the same region at the same time.
The reflection of a wave at the edge of a medium is an example of
boundary conditions. In the case of a string, if the string is fixed at the boundary, the reflected pulse moves in the opposite direction, but the vertical direction of the wave is inverted. If the string is free to move at the boundary (if it is attached to a ring around a pole, for example), then the reflected wave is
not inverted.
The wave that results from interference is equal to the sum of each contributing wave. This is called the
principle of superposition. If the total wave function is labeled
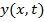
, and this wave is the result of interference between two waves labeled
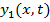
and
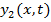
, then the formula for the total wave is,
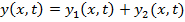 Standing Waves
Standing Waves
When a sinusoidal wave hits a boundary, it is reflected. By the principle of superposition, the resulting wave is the sum of the reflected and original waves. In the case of a sinusoidal transverse wave on a string, the result of the superposition is a
standing wave. The sum of the reflected and original waves results in points in the wave pattern where the string does not move. These are
called nodes. Around the nodes, the wave fluctuates up and down. Midway between the nodes, the positions where the string reaches maximum amplitude are called
antinodes. At the nodes, the original and reflected waves cancel each other. This cancellation is called
destructive interference. The sum of the two components of the waves results in a decreased amplitude. At the antinodes, the original and reflected waves sum to produce a larger wave. This is called
constructive interference. The amplitude of the two components of the wave is greater than the original amplitude. The distance between successive nodes (or antinodes) is half of the wavelength,
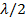
.
If the amplitude of the original wave is A, the wave function for the standing wave is,
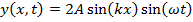
The amplitude of the standing wave
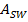
is equal to twice the amplitude of the original wave,
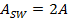
The positions of the nodes are the positions where
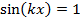
. This happens when x has values,
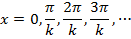
These positions of the nodes x can also be written in terms of the wavelength
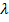
,
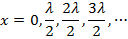 Harmonics, Fundamental Frequencies, and Normal Modes
Harmonics, Fundamental Frequencies, and Normal Modes
Standing waves are produced when one end of a string is fixed. If both ends of a string are fixed, standing waves can only form if certain conditions are met. The location of the nodes on a string fixed and both ends depends on the length of the string, represented with the letter L. Both ends of the string must be a node, and the other nodes are spaced half of the wavelength apart. If the letter n represents the number of a certain node, the formula relating the nodes to the length of the string is,
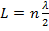
where
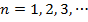
This formula can be rearranged to solve for the wavelengths
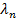
that allow standing waves,
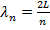
where
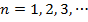
If the wavelength is not equal to one of these values, standing waves will not form. The wave speed must be the same for a certain string, and so the formula for wave speed can be used to find the frequencies f
n at which standing waves can form,
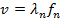
The formula for the frequencies is,
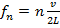
where
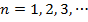
The frequency with n = 1 is called the
fundamental frequency of the string. The fundamental frequency is,
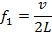
Every other frequency at which a standing wave can form is a multiple of the fundamental frequency,
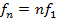
where
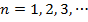
The frequencies f
n are called
harmonics. The series of frequencies is called a
harmonic series. The frequencies above the fundamental frequency (n = 2,3,...) are sometimes called
overtones.
A
normal mode of a sinusoidal wave is a situation where all of the particles of the medium move with the same frequency. For a string of length L fixed at both ends, the normal modes correspond to the harmonic frequencies.
The formula for the fundamental frequency of a string can also be written in terms of the linear mass density and the tension in a string. The formula for wave speed from earlier in this section,
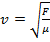
, can be substituted in to the formula for the fundamental frequency,
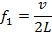
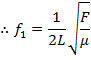
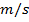 . The wave speed depends entirely on the choice of medium. For a given medium, the wave speed will always be the same.
. The wave speed depends entirely on the choice of medium. For a given medium, the wave speed will always be the same.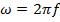
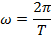
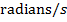 .
.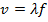
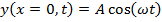
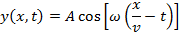
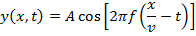
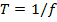 , and the formula relating the wave speed and wavelength
, and the formula relating the wave speed and wavelength 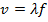 , the wave function can also be written,
, the wave function can also be written,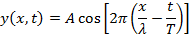
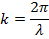
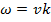
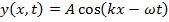
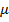 ("mu"), and has units of
("mu"), and has units of 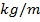 . It can be shown that the wave speed depends only on the tension in the string, and the linear mass density,
. It can be shown that the wave speed depends only on the tension in the string, and the linear mass density,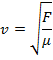
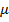 , the angular velocity
, the angular velocity 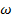 , and the amplitude of the wave A. The formula for average power
, and the amplitude of the wave A. The formula for average power 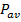 for a sinusoidal wave on a string is,
for a sinusoidal wave on a string is,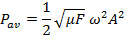
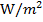 . If a wave spreads out in all directions from a source, the intensity at a certain distance is inversely proportional to the square of the distance. This means that at a distance r, the intensity is related to
. If a wave spreads out in all directions from a source, the intensity at a certain distance is inversely proportional to the square of the distance. This means that at a distance r, the intensity is related to 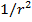 . If the power of the wave is P, then the intensity at distance r is,
. If the power of the wave is P, then the intensity at distance r is,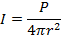
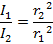
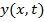 , and this wave is the result of interference between two waves labeled
, and this wave is the result of interference between two waves labeled 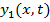 and
and 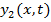 , then the formula for the total wave is,
, then the formula for the total wave is,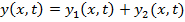
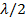 .
.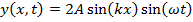
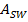 is equal to twice the amplitude of the original wave,
is equal to twice the amplitude of the original wave,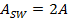
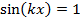 . This happens when x has values,
. This happens when x has values,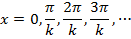
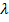 ,
,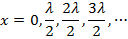
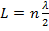 where
where 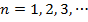
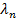 that allow standing waves,
that allow standing waves,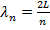 where
where 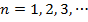
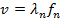
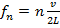 where
where 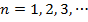
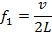
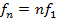 where
where 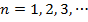
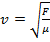 , can be substituted in to the formula for the fundamental frequency,
, can be substituted in to the formula for the fundamental frequency,