The Ambiguous Case of the Law of Sines
For example, take a look at this picture:
If you are told that
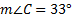, b = 10 in. and c= 6 in, there are two different triangles that match this criteria. As you can see in the picture, either an acute triangle or an obtuse triangle could be created because side c could swing either in or out along the unknown side a.When you are given two sides and an angle not in between those sides, you need to be on the lookout for the ambiguous case.
To determine if there is a 2nd valid angle:
1. See if you are given two sides and the angle not in between (SSA). This is the situation that may have 2 possible answers.
2. Find the value of the unknown angle.
3. Once you find the value of your angle, subtract it from 180° to find the possible second angle.
4. Add the new angle to the original angle. If their sum is less than 180°, you have two valid answers. If the sum is over 180°, then the second angle is not valid.
2. Find the value of the unknown angle.
3. Once you find the value of your angle, subtract it from 180° to find the possible second angle.
4. Add the new angle to the original angle. If their sum is less than 180°, you have two valid answers. If the sum is over 180°, then the second angle is not valid.
Examples:
1. Use the Law of Sines to find the measure of angle B from our example in which 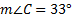, b = 10 in. and c = 6 in
2. Use the Law of Sines to find measure of angle A in this scenario: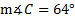
c = 10 ft. a = 8 ft.
If it helps, you can draw a rough sketch to view this triangle, but this is optional. We know that this triangle is a candidate for the ambiguous case since we are given two sides and an angle not in between them.
We need to find the measure of angle B using the Law of Sines:
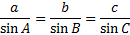
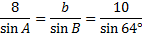
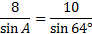
Now we'll cross multiply and solve the equation:
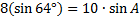
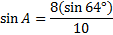
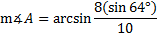
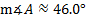
We've found one value for angle A, but we need to see if there's another possible value. To do this, we'll subtract 46.0° from 180°.
To see if 134° is a valid answer, we must add this to the other existing angle. If their sum is less than 180°, we know a triangle can exist. If, however, it is over 180°, then it is not a valid answer.
Final answer: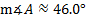
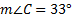, b = 10 in. and c = 6 in
First we know that this triangle is a candidate for the ambiguous case since we are given two sides and an angle not in between them.
We need to find the measure of angle B using the Law of Sines:
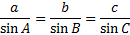
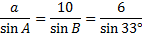
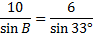
Now we'll cross multiply and solve the equation:
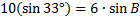
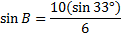
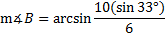
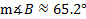
We've found one value for angle B, but we need to see if there's another possible value. To do this, we'll subtract 65.2° from 180°.
To see if 114.8° is a valid answer, we must add this to the other existing angle. If their sum is less than 180°, we know a triangle can exist. If, however, it is over 180°, then it is not a valid answer (because the three angles of a triangle must add up to 180°.)
Final answer: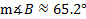 and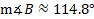 
We need to find the measure of angle B using the Law of Sines:
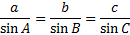
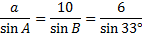
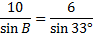
Now we'll cross multiply and solve the equation:
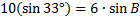
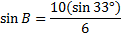
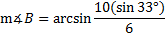
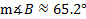
We've found one value for angle B, but we need to see if there's another possible value. To do this, we'll subtract 65.2° from 180°.
180° - 65.2° = 114.8°
To see if 114.8° is a valid answer, we must add this to the other existing angle. If their sum is less than 180°, we know a triangle can exist. If, however, it is over 180°, then it is not a valid answer (because the three angles of a triangle must add up to 180°.)
114.8° + 33° = 147.8°
Since 147.8° is less than 180°, we know that 114.8° is a valid answer
Since 147.8° is less than 180°, we know that 114.8° is a valid answer
Final answer:
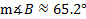and 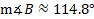2. Use the Law of Sines to find measure of angle A in this scenario:
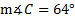c = 10 ft. a = 8 ft.
If it helps, you can draw a rough sketch to view this triangle, but this is optional. We know that this triangle is a candidate for the ambiguous case since we are given two sides and an angle not in between them.We need to find the measure of angle B using the Law of Sines:
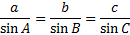
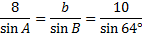
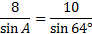
Now we'll cross multiply and solve the equation:
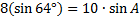
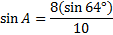
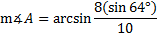
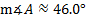
We've found one value for angle A, but we need to see if there's another possible value. To do this, we'll subtract 46.0° from 180°.
180° - 46° = 134°
To see if 134° is a valid answer, we must add this to the other existing angle. If their sum is less than 180°, we know a triangle can exist. If, however, it is over 180°, then it is not a valid answer.
134° + 64° = 198°
Since 198° is greater than 180°, we know the second measurement of 134° is not a valid answer.
Since 198° is greater than 180°, we know the second measurement of 134° is not a valid answer.
Final answer:
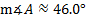
Practice: Use the Law of Sines to find the angle. Be careful to check for the ambiguous case if needed. Round all answers to the nearest tenth.
1.Find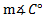
if 
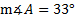a = 9 ft. c = 7 ft.
2.Find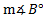
if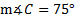 
b = 4 in. c = 5 in.
3.Find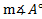
if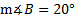 
a = 5 cm. b = 3 cm.
4.Find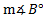 if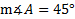 
a = 8 m. b = 10 m.
5.Find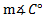 if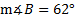 
b = 12 mm. c = 9 mm.
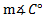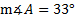if a = 9 ft. c = 7 ft.2.Find
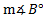if 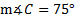b = 4 in. c = 5 in.3.Find
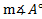if 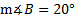a = 5 cm. b = 3 cm.4.Find
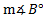if 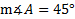a = 8 m. b = 10 m.5.Find
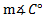if 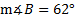b = 12 mm. c = 9 mm.Answers: 1) 25.1° 2) 50.6° 3) 35.8° and 144.2° 4) 62.1° and 117.9° 5) 41.5°
|
Related Links: Math Fractions Factors |