Home > Math > Pre Calculus > Scalar Multiplication and Vector Addition

Scalar Multiplication and Vector Addition

The two basic vector operations are scalar multiplication and vector addition. In general, when working with vectors numbers or constants are called scalars.

Scalar Multiplication is when a vector is multiplied by a scalar (a number or a constant). If a vector v is multiplied by a scalar k the result is kv. If k is positive then kv will have the same directions as v. If k is negative, kv will have the opposite direction as v.

SCALAR MULTIPLICATION:


Let v = 〈 v 1 , v 2 〉 and k be a scalar.


kv = k 〈 v 1 , v 2 〉 = 〈k v 1 ,k v 2 〉



To add two vectors u and v, place the initial point of the second vector (without changing length or direction) on the terminal point of the first vector. Then join the initial point of the first vector to the terminus of the second vector. This joining line represents the sum of the two vectors.



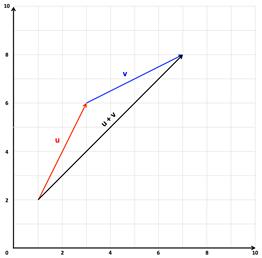
The sum of vectors u and v in component form is:

ADDITION OF VECTORS:


Let u = 〈 u 1 , u 2 〉 and v = 〈 v 1 , v 2 〉


u+v=〈 u 1 + v 1 ,  u 2 + v 2 〉


u−v=u+( −v )=〈 u 1 − v 1 ,  u 2 − v 2 〉



Scalar multiplication and vector addition share the following properties:

PROPERTIES OF SCALAR MULTIPLICATION AND VECTOR ADDITION:

Let u,v and w be vectors and c and d be scalars.


1. u + v = v + u2. (u + v) + w = u + (v + w)

3. u + 0 = u  4. u + (-u) = 0

5. c(du) = (cd)u6. (c + d)u = cu + du

7. c(u + v) = cu + cv    8. 1 · u = u, 0 · u = 0

9. ||cv|| = |c|||v||


Let's look at a couple examples.

Example 1: If u=〈−2,1〉 and v=〈7,−3〉 find (a) u + v and (b) u - v.

Step 1: Calculate u + v using vector addition.


Add the x-component of both vectors. Do the same for the y-components.

u+v=〈−2+7, 1+( −3 )〉


u+v=〈5,−2〉

Step 2: Calculate u - v using vector addition.


Remember u - v = u + (-v), therefore subtract the x-component of v from u. Do the same for the y-components.

u−v=u+( −v )=〈−2−7, 1−( −3 )〉


u−v=〈−9, 4〉

Example 2: If u=〈6,15〉 and v=〈−5,20〉 find (a) 2u + v and (b) 5u - 2v.

Step 1: Calculate 2u + v using scalar multiplication and vector addition.


a) First calculate 2u using scalar multiplication.


b) Next calculate 2u+v using vector addition.

2u=2〈6,15〉=〈2 ·6, 2 ·15〉


2u=〈12, 30〉


2u+v=〈12+( −5 ), 30+20〉


2u+v=〈7,50〉

Step 2: Calculate 5u - 2v using scalar multiplication and vector addition.


a) First calculate 5u and 2v using scalar multiplication.


b) Next calculate 5u+2v using vector addition.

5u=5〈6,15〉=〈5 ·6, 5 ·15〉


5u=〈30, 75〉


2v=2〈−5,20〉=〈2 ·( −5 ), 2 ·20〉


2u=〈−10, 40〉


5u−2v=5u+( −2v )


5u−2v=〈30−( −10 ), 75−40〉


5u−2v=〈40, 35〉





Related Links:
Math
algebra
Unit Vectors
Direction Angles of Vectors
Pre Calculus


To link to this Scalar Multiplication and Vector Addition page, copy the following code to your site: