Binding Energy Formula
Definition: The binding energy is the energy required to disassemble or separate a nucleus into its nucleons. The nucleons are the protons and neutrons and other nuclear particles that form the nucleus of any atom. The nucleons are kept together through forces called the strong nuclear forces and the more thigh the nucleus components are bound, the greater the binding energy required to separate them.
General Formula: The binding energy (also known as BE) is related to the Einstein's equation E = mc2:
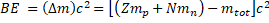
Where is called mass defect and it is the difference of the mass after the nucleus is separated. Since Z is the number the protons and N the number of neutrons, the nucleus mass should the sum of both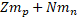 
and this sum minus the total mass when the particles are together (
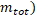is the resulting mass defect and c is the speed of light with the value c = 2.9979 x 108 m/s.
Use: The binding energy is used to make calculation in nuclear physics. It is very useful in the fields of nuclear fusion and nuclear fission. These both areas study the light nuclei fuse or nuclei split and it is used to generate electricity or even nuclear weapon.
Example: Find the binding energy of a beryllium-4 nucleus if its mass of the nucleus is 9.012182 u.
a) First step is to calculate the mass defect of beryllium. This atom has 4 protons (mass of 1 proton is 1.00728 amu) and 5 neutrons (mass of each neutron is 1.00867 amu/neutron:
b) [4 proton (1.00728 u) + 5 neutron (1.00867 u)] - 9.012182 u = 0.060288 u x 1.6606 x 10-27 kg/amu = 1.00114 x 10-28 kg/nucleus
c) And the binding energy is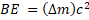 
= 0.060288 u (2.9979 x 108 m/s)2 = 8.9976 x 10-12 J/nucleus
Considerations: The units are the units of energy (Joules or eV) per nucleus. It should be observed, the total mass of a nucleus when the nucleons are together is smaller than the sum of the particles separated. It is invariable for all the atoms.
|
Related Links: |