Acceleration Due to Gravity Formula

Near the Earth's surface, the acceleration due to gravity is approximately constant. However, at large distances from the Earth, or around other planets or moons, the acceleration is different. The acceleration due to gravity depends on the mass of the body, the distance from the center of mass, and a constant G, which is called the "universal gravitational constant". Its value is = 6.673 x 10^-11 N·m²/kg².

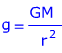
g = acceleration due to gravity (units m/s²)

G = the universal gravitational constant, G = 6.673 x 10^-11N·m²kg²

m = mass of a large body (for example, Earth)

r = the distance from the center of mass of the large body

Acceleration Due to Gravity Formula Questions:

1) The radius of the moon is 1.74 x 10⁶ m. The mass of the moon is 7.35 x 10²² kg. Find the acceleration due to gravity on the surface of the moon.

Answer: On the surface of the moon, the distance to the center of mass is the same as the radius: r = 1.74 x 10⁶ m = 1 740 000 m. The acceleration due to gravity on the surface of the moon can be found using the formula:

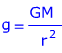
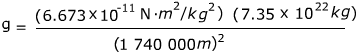
g = 1.620 m/s²

The acceleration due to gravity on the surface of the moon is 1.620 m/s².

2) The radius of the Earth is 6.38 x 10⁶ m. The mass of the Earth is 5.98x 10²⁴ kg. If a satellite is orbiting the Earth 250 km above the surface, what acceleration due to gravity does it experience?

Answer: The acceleration due to gravity depends on the distance from the center of mass of the large body to the satellite. This distance is the sum of the radius of the Earth and the distance from the satellite to the surface:

r =(6.38 x 10⁶ m) + (250 km)

r = 6 380 000 + 250 000 m

r = 6 630 000 m

The acceleration due to gravity of the satellite can be found from the formula:

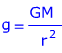
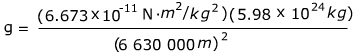
g = 9.078 m/s²

The acceleration due to gravity at the height of the satellite, 250 km above the surface of the Earth, is 9.078 m/s².