Angular Momentum Formula(Moment of Inertia and Angular Velocity)

Angular momentum relates to how much an object is rotating. An object has a constant angular momentum when it is neither speeding up nor slowing down. The angular momentum of an object depends on the distribution of the mass of the object. The moment of inertia is a value that describes the distribution. It can be found by integrating over the mass of all parts of the object and their distances to the center of rotation, but it is also possible to look up the moments of inertia for common shapes. The angular momentum is the product of the moment of inertia and the angular velocity around an axis.The units of angular momentum are kg∙m²/s.

angular momentum = (moment of inertia)(angular velocity)

L = Iω

L = angular momentum (kg∙m²/s)

I = moment of inertia (kg∙m²)

ω = angularvelocity (radians/s)

Angular Momentum Formula Questions:

1) A DVD disc has a radius of 0.0600 m, and a mass of 0.0200 kg. The moment of inertia of a solid disc is 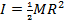, where M is the mass of the disc, and R is the radius. When a DVD in a certain machine starts playing, it has an angular velocity of 160.0 radians/s. What is the angular momentum of this disc?

Answer: The angular momentum can be found using the formula, and the moment of inertia of a solid disc (ignoring the hole in the middle). The angular momentum is:

L = Iω

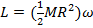
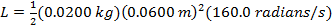
L = 0.00576 kg∙m²/s

The angular momentum of this DVD disc is 0.00576 kg∙m²/s.

2) A basketball spinning on an athlete's finger has angular velocity ω = 120.0 rad/s. The moment of inertia of a hollow sphere is 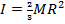, where M is the mass and R is the radius. If the basketball weighs 0.6000 kg and has a radius of 0.1200 m, what is the angular momentum of the basketball?

Answer:The angular momentum of the basketball can be found using the moment of inertia of a hollow sphere, and the formula. The angular momentum is:

L = Iω

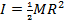
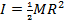
L = 0.6912 kg∙m²/s

The angular momentum of the spinning basketball is 0.6912 kg∙m²/s.