Average Angular Velocity Formula
The angular velocity of a rotating object is the rate at which the angular coordinate changes with respect to time. The angular coordinate is the angle of the object relative to a certain coordinate system, and is usually represented with the Greek letter θ ("theta"). The average angular velocity is the change in the angular coordinate θ, expressed in radians, divided by the change in time. The angular velocity is a vector that points in the direction of the axis of rotation. The magnitude of the angular velocity is given by the formula below. The unit of angular velocity is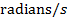 
.
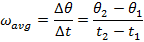
= average angular velocity, ()
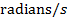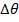= change in angular coordinate (radians)
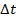= change in time (s)
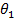= initial angular coordinate (radians)
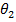= final angular coordinate (radians)
t1 = initial time (s)
t2 = final time (s)
Average Angular Velocity Formula Questions:
1) The pendulum of a large grandfather clock swings between angles of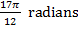 
and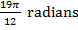 
. It swings from one angle to the other in 1.00 seconds. What is the average angular velocity of the pendulum as it swings from one angle to the other?
Answer: The change in time between the two angular coordinate values is given as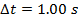 
. The initial angular coordinate is 
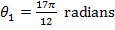, and the final angular coordinate is 
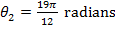. The average angular velocity can be found using the formula:
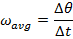
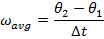
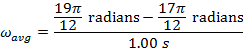
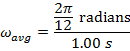
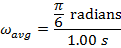
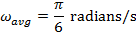
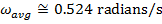
Between the initial and final angles, the average angular velocity of the clock's pendulum was 
, which is approximately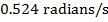 
.
2) A powerful fan blade spins at an average angular velocity of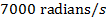 
. How long does it take, in seconds, to rotate 
?
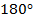Answer: The change in the angular coordinate requested in this problem is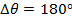 
. The first step to answering this problem is to convert from degrees to radians. A full circle consists of 
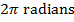, or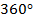 
. The change in the angular coordinate is therefore:
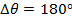
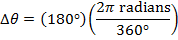
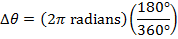
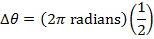
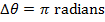
The time required for the fan to rotate by this amount can be found by rearranging the average angular velocity formula:
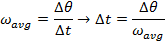
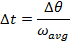
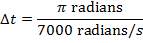
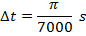
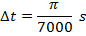
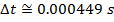
The time required for the fan to rotate 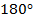is only 
.
|
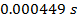Related Links: |